В геометрии существуют различные вопросы, требующие анализа и решения. Один из таких вопросов - сколько плоскостей может проходить через три точки?
Для ответа на этот вопрос, необходимо понять основные принципы геометрии и свойства плоскостей. Каждая плоскость определяется тремя неколлинеарными точками. Это значит, что выбирая любые три точки, которые не находятся на одной прямой, можно определить плоскость, проходящую через них.
Первый вариант - все три точки являются коллинеарными, то есть лежат на одной прямой. В этом случае, существует только одна плоскость, которая проходит через эти точки. Это объясняется тем, что определение плоскости требует, чтобы три точки не лежали на одной прямой.
Второй вариант - третья точка не лежит на прямой, образованной двумя другими точками. В этом случае, через эти три точки можно провести бесконечное количество плоскостей. Каждая плоскость, проходящая через две заданные точки, будет пересекать третью точку и образовывать уникальную плоскость. Таким образом, количество плоскостей, проходящих через три точки, будет равно бесконечности.
Таким образом, ответ на вопрос "Сколько плоскостей может проходить через три точки?" зависит от того, являются ли выбранные точки коллинеарными или нет. В первом случае, будет существовать только одна плоскость, проходящая через них, во втором - бесконечное количество плоскостей.
Определение плоскости в геометрии
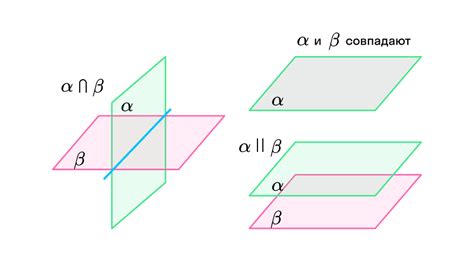
В геометрии плоскость определяется тремя точками, непринадлежащими одной прямой. Если заданы три точки A, B и C, то через них можно провести единственную плоскость.
При определении плоскости важно также учесть, что она может быть вертикальной, горизонтальной или наклонной, в зависимости от ориентации точек в пространстве.
В геометрии плоскость обозначается большой буквой, например, P. Точки на плоскости обычно обозначаются заглавными латинскими буквами, например, A, B и C.
Плоскость играет важную роль в геометрии и используется для описания и визуализации различных объектов, таких как фигуры, поверхности и пространства.
Какие данные нужны для определения плоскости?

Для определения плоскости в трехмерном пространстве необходимы три непротивоположно направленных вектора, три точки или два вектора и одна точка.
В случае, если имеются три непротивоположно направленных вектора, например, векторы AB, AC и AD, можно построить плоскость, проходящую через эти три точки. Уравнение плоскости в данном случае будет иметь вид: ax + by + cz + d = 0, где (a, b, c) - коэффициенты нормального вектора к плоскости, и (x, y, z) - координаты точки, лежащей на плоскости.
Если имеются два вектора, например, векторы AB и BC, и одна точка, например, точка A, можно также определить плоскость, проходящую через эти три точки. Для этого можно воспользоваться скалярным произведением и векторным произведением данных векторов. Получив нормальный вектор к плоскости, можно составить уравнение плоскости, аналогично предыдущему случаю.
Основные раздражители воздуха

Один из основных раздражителей воздуха - это загрязнение, вызванное промышленными выбросами, автотранспортом и бытовым отоплением. Вредные вещества, такие как оксиды азота и серы, угарный газ и твердые частицы, могут накапливаться в воздухе и создавать проблемы для дыхательной системы. Одним из способов снизить воздействие этих раздражителей является использование экологически чистых источников энергии и технологий.
Другим важным раздражителем воздуха является аллергены. Пыль, пыльцы, грибки и другие микроорганизмы могут вызывать аллергические реакции у людей, особенно у тех, кто страдает от аллергических заболеваний, таких как астма или насморк. Систематическая уборка, использование фильтров и хорошая вентиляция помогают уменьшить присутствие аллергенов в воздухе.
Также стоит упомянуть о табакокурении как одном из основных раздражителей воздуха. Дым от сигарет содержит множество вредных соединений, которые могут оказывать отрицательное воздействие на окружающих. Курение в присутствии других людей, особенно детей и беременных женщин, является особенно опасным. Отказ от курения и создание курительных зон помогут снизить воздействие табачного дыма на окружающих.
Плоскость, проходящая через три неколлинеарные точки

Чтобы определить плоскость, проходящую через три точки, необходимо решить следующую систему линейных уравнений:
- Уравнение плоскости: Ax + By + Cz + D = 0
- Условие прохождения первой точки: Ax1 + By1 + Cz1 + D = 0
- Условие прохождения второй точки: Ax2 + By2 + Cz2 + D = 0
- Условие прохождения третьей точки: Ax3 + By3 + Cz3 + D = 0
Где (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3) – координаты трех неколлинеарных точек.
Решив эту систему уравнений, можно получить коэффициенты A, B, C и D и, таким образом, определить уравнение плоскости.
Итак, плоскость, проходящая через три неколлинеарные точки, может быть однозначно задана уравнением Ax + By + Cz + D = 0, где A, B, C и D – коэффициенты, полученные после решения системы уравнений.
Плоскость, проходящая через две пересекающиеся прямых
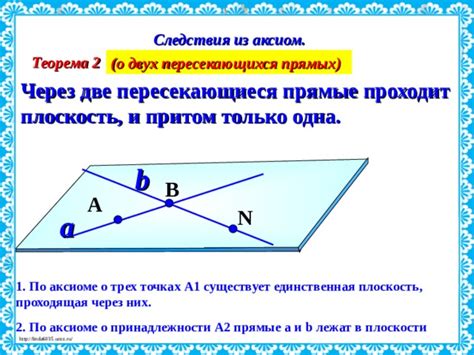
Когда имеется две пересекающиеся прямые, можно провести через них бесконечное множество плоскостей. Возьмем две прямые, обозначим их как AB и CD.
Чтобы найти плоскость, проходящую через эти две прямые, необходимо найти нормальные векторы каждой из них. Нормальный вектор - это вектор, перпендикулярный прямой.
Пусть вектор AB = (a, b, c), а вектор CD = (d, e, f).
Плоскость, проходящая через AB и CD, будет иметь нормальный вектор, равный векторному произведению данных векторов:
(a, b, c) × (d, e, f) = (bf - ce, cd - af, ae - bd).
Таким образом, получаем нормальный вектор (bf - ce, cd - af, ae - bd), который определяет плоскость, проходящую через две пересекающиеся прямые AB и CD.
Плоскость, параллельная двум пересекающимся прямым
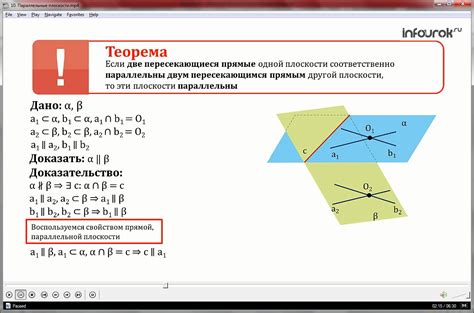
Плоскость, параллельная двум пересекающимся прямым, может проходить через три точки, если эти три точки лежат в одной плоскости и не лежат на одной прямой.
Для построения такой плоскости необходимо определить две пары прямых, пересекающихся между собой, и найти точку пересечения этих прямых.
Применяя правило построения плоскости через три точки, можно построить плоскость, параллельную двум пересекающимся прямым.
Итак, плоскость, параллельная двум пересекающимся прямым, может проходить через три точки, если эти три точки лежат в одной плоскости и не лежат на одной прямой.
Плоскость, проходящая через три коллинеарные точки

Условие, при котором три точки считаются коллинеарными, состоит в том, что все они лежат на одной прямой и не совпадают друг с другом. Таким образом, плоскость, проходящая через такие точки, будет иметь нулевую толщину и будет представлять собой всего лишь прямую.
В случае, когда три точки расположены на одной прямой, невозможно определить плоскость, проходящую через них, так как такая плоскость будет вырожденной. В этом случае, всегда будет существовать бесконечное количество плоскостей, проходящих через эти три точки.
Таким образом, при обсуждении плоскостей, проходящих через три коллинеарные точки, следует отметить, что такие плоскости не имеют конкретной формы или ориентации, так как они являются вырожденными и представляют собой всего лишь прямые. В этой ситуации важно понимать, что нет одной единственной плоскости, проходящей через такие точки, и что они могут быть представлены множеством плоскостей, все проходящих через те же коллинеарные точки.
Нестандартные случаи
В рассмотренных примерах мы рассмотрели типичные случаи, но иногда возможны и более необычные ситуации.
Если три точки лежат на одной прямой, то через них можно провести бесконечное количество плоскостей. В этом случае все плоскости будут параллельны данной прямой.
Если же три точки лежат на разных прямых, но эти прямые пересекаются в одной точке, то через них также можно провести бесконечное количество плоскостей. В этом случае все плоскости будут проходить через эту общую точку пересечения.
Также возможен случай, когда три точки лежат на плоскости, которая параллельна данной плоскости. В этом случае через эти точки нельзя провести ни одной плоскости.
В зависимости от расположения точек могут возникать и другие интересные и нестандартные случаи, которые требуют отдельного анализа и рассмотрения.
Три точки, лежащие на одной прямой

Если три точки лежат на одной прямой, то существует неограниченное количество плоскостей, проходящих через эти точки.
Для наглядности, допустим, что у нас есть точки A, B и C, которые лежат на одной прямой. Плоскость, проходящая через эти три точки, может быть представлена как плоскость XY, где точка A имеет координаты (xA, yA), точка B - (xB, yB), а точка C - (xC, yC).
Так как точки лежат на одной прямой, то координаты этих точек удовлетворяют следующему соотношению:
- (yB - yA)/(xB - xA) = (yC - yA)/(xC - xA)
Из этого уравнения следует, что проходящие через точки A, B и C плоскости можно представить формулой:
(y - yA)/(x - xA) = (yB - yA)/(xB - xA)
Эта формула описывает все возможные плоскости, проходящие через точки A, B и C. Кроме того, для любого значения x и y, удовлетворяющего этой формуле, существует плоскость, проходящая через эти точки.



