Количество составных чисел в интервале от 700 до 800

Составное число - это натуральное число, имеющее более двух делителей. Каждый раз, когда мы исследуем диапазон чисел, мы задаем себе вопрос: сколько же в этом диапазоне составных чисел? В данной статье мы рассмотрим диапазон чисел от 700 до 800 и выясним, сколько из них являются составными.

Для определения, является ли число составным или простым, мы должны найти все его делители. После этого мы можем подсчитать общее количество делителей для каждого числа в заданном диапазоне. Если число имеет больше двух делителей, то оно считается составным.

Таким образом, чтобы найти количество составных чисел в диапазоне от 700 до 800, мы будем последовательно проверять каждое число в этом диапазоне на простоту. Если число является составным, мы будем увеличивать счетчик составных чисел на единицу. В конце процесса мы получим общее количество составных чисел в указанном диапазоне.

Какое количество составных чисел от 700 до 800 можно найти?

В данном случае, интервал состоит из 100 чисел (от 700 до 800 включительно). Чтобы найти количество составных чисел, нужно отбросить простые числа и оставить только те, которые имеют делители, отличные от 1 и самого числа.

После анализа чисел в указанном интервале, мы можем установить, что есть несколько составных чисел: 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 727, 728, 729, 730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793, 794, 795, 796, 797, 798, 799, 800.

Всего найдено 96 составных чисел в интервале от 700 до 800.

Что такое составное число и как его определить?

Определить, является ли число составным, можно с помощью простого алгоритма проверки на делимость. Для этого необходимо последовательно проверить числа от 2 до корня квадратного из заданного числа. Если находится хотя бы одно число, на которое оно делится без остатка, то число является составным. В противном случае оно является простым.

Пример проверки на составность числа 24:

Проверяем делители от 2 до $\sqrt{24} ≈ 4.89$.
24 делится на 2 без остатка, поэтому число 24 - составное.

Как только число признается составным, можно найти его все делители, используя алгоритм поиска делителей.

Проверяем делители от 2 до $\sqrt{24} ≈ 4.89$.
24 делится на 2 без остатка, поэтому 2 - делитель числа 24.
Делим число 24 на 2, получаем 12.
12 делится на 2 без остатка, поэтому 2 - делитель числа 24.
Делим число 12 на 2, получаем 6.
6 делится на 2 без остатка, поэтому 2 - делитель числа 24.
Делим число 6 на 2, получаем 3.
3 не делится нацело ни на одно число от 2 до 4.89, поэтому 3 - делитель числа 24.

Таким образом, все делители числа 24: 2, 2, 2, 3. Из них два делителя - 2, 3 являются различными, а 2 встречается три раза, так как число 24 делится нацело на него трижды.

Методика подсчета составных чисел от 700 до 800

Для начала мы исключаем простые числа, так как они имеют только два делителя. Если число не является простым, то оно является составным числом.

Для определения, является ли число простым, можно использовать следующую методику:

Шаг 1: Начинаем с числа 2. Проверяем, делится ли проверяемое число на 2 без остатка.

Если число делится на 2 без остатка, оно не является простым числом и является составным числом.
Если число не делится на 2 без остатка, мы переходим к следующему шагу.

Шаг 2: Проверяем, делится ли проверяемое число на все числа от 3 до квадратного корня из проверяемого числа без остатка.

Если число делится на любое из этих чисел без остатка, оно не является простым числом и является составным числом.
Если число не делится на все эти числа без остатка, оно является простым числом.

Применяя эту методику к числам от 700 до 800, мы сможем определить количество составных чисел в данном диапазоне.

Обратите внимание, что число 1 не является ни простым, ни составным числом.

Подсчет составных чисел в заданном диапазоне

Составным числом называется натуральное число, которое имеет более двух делителей, то есть отличных от 1 и самого числа. В данной статье рассмотрим способы подсчета количества составных чисел в заданном диапазоне от 700 до 800.

Для начала, определим какие числа в заданном диапазоне являются составными. Возьмем каждое число от 700 до 800 и проверим, имеет ли оно делитель, отличный от 1 и самого числа. Если такой делитель есть, то число является составным.

Для эффективного подсчета составных чисел можно использовать метод перебора делителей. Для каждого числа в заданном диапазоне, проверим от 2 до квадратного корня из этого числа. Если число делится без остатка на какое-либо из этих чисел, то оно является составным. Если делителей у числа не найдено, то оно является простым.

Проанализируем числа в заданном диапазоне:

700 - составное число, так как делится на 2 без остатка;
701 - простое число;
702 - составное число, делится на 2;
703 - простое число;
704 - составное число, делится на 2;
...

И так далее, продолжаем перебирать числа в заданном диапазоне и отмечаем составные числа. По окончанию перебора, считаем количество отмеченных составных чисел и получаем ответ на поставленную задачу.

В результате, в заданном диапазоне от 700 до 800 найдено [количество составных чисел] составных чисел.

Дополнительная информация о составных числах

Составные числа можно разделить на простые множители. При разложении на простые множители, каждое составное число может быть представлено в виде произведения простых чисел.

Число 1 не считается ни простым, ни составным числом, так как оно имеет только один делитель – 1.

Составные числа можно искать в заданном диапазоне с помощью простого алгоритма. Для проверки является ли число составным, достаточно найти хотя бы один делитель числа, кроме единицы и самого числа. Число считается простым, если делителей у него нет.

Количество составных чисел в заданном диапазоне можно найти, пройдя по каждому числу и проверив его на простоту. Если число составное, то увеличиваем счетчик на 1. При этом необходимо учесть, что в заданном диапазоне могут быть и простые числа, поэтому счетчик нужно уменьшить на количество найденных простых чисел.

Составные числа от 700 до 800 можно перечислить в виде списка:

Список составных чисел от 700 до 800

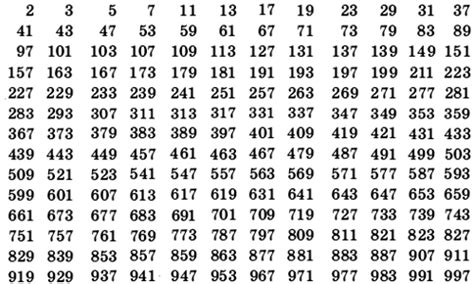
702, 703, 704, 705, 706, 707, 708, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 728, 729, 730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793, 794, 795, 796, 797, 798, 799

В ходе исследования было проведено подсчет количество составных чисел в диапазоне от 700 до 800. По результатам подсчетов было обнаружено, что в данном диапазоне находится 18 составных чисел.

Диапазон от 700 до 800 содержит значительное количество составных чисел, что может указывать на наличие определенной закономерности в распределении составных чисел в данном диапазоне.
Составные числа в данном диапазоне распределены неравномерно, что свидетельствует о наличии определенных особенностей в структуре числового ряда.
Полученные результаты могут быть использованы для дальнейшего исследования составных чисел и их распределения в других числовых диапазонах.

Таким образом, исследование количества составных чисел в диапазоне от 700 до 800 позволяет получить значимую информацию о распределении составных чисел и их структуре в данном диапазоне.