Математика - это наука о числах, формулах, геометрии и многом другом. Одним из интересных вопросов, которые мы можем рассмотреть, является количество кривых линий, которые могут быть построены между двумя заданными точками.
Когда мы говорим о кривых линиях, мы можем иметь в виду графики функций, спирали, эллипсы и т.д. Эти кривые могут быть сконструированы с использованием различных математических формул и алгоритмов. Однако, вопрос о количестве возможных кривых линий между двумя точками является довольно сложным и не всегда имеет простой ответ.
В общем случае, количество кривых линий между двумя точками зависит от множества факторов, таких как координаты точек, тип кривой, ограничения и условия, накладываемые на кривую. Например, если мы рассматриваем прямую линию, то количество возможных линий будет бесконечным, так как мы можем изменять ее наклон и положение.
Что такое количество кривых линий?

Количество кривых линий может быть использовано в различных областях, таких как:
- Финансы и экономика для отслеживания изменений на рынке или в индексах ценных бумаг.
- Наука и исследования для изучения динамики природных процессов или поведения физических систем.
- Маркетинг и бизнес для анализа трендов и изменений в поведении потребителей.
- Технологии для отслеживания эффективности программного обеспечения или аппаратного обеспечения.
Зная, что представляют собой кривые линии и как они работают, можно лучше понять и анализировать данные в различных областях знаний и получить ценные знания для принятия решений.
От чего зависит количество кривых линий?

Количество кривых линий между двумя точками зависит от различных факторов.
Первый и основной фактор - это форма и расположение препятствий на пути между точками. Если между точками находятся препятствия, такие как стены, здания или горы, то количество кривых линий будет больше. Чем больше препятствий на пути, тем сложнее будет найти прямую линию между точками, и вместо нее придется использовать несколько кривых линий.
Второй фактор - это условия перемещения по местности. Если перемещение ограничено определенными правилами или требует специфических навыков, то количество кривых линий также может увеличиться. Например, в гористых или лесистых местностях может потребоваться обходить препятствия, что приведет к появлению дополнительных кривых линий.
Третий фактор - это масштаб рассматриваемой территории. Чем меньше масштаб, тем более детальную карту мы имеем, и тем более точно мы можем определить путь между точками. В таком случае количество кривых линий будет минимальным.
Наконец, четвертый фактор - это выбранная система координат или способ измерения пути. В разных системах координат могут быть различные методы измерения и определения пути между точками, что может привести к разным количествам кривых линий.
В итоге, количество кривых линий между двумя точками зависит от взаимодействия всех вышеперечисленных факторов и может быть разным в каждом конкретном случае.
Как вычислить количество кривых линий?

Вычисление количества кривых линий между двумя точками может быть полезным при решении различных задач в математике и геометрии. Вот несколько способов, которые помогут вам это сделать.
Способ 1: Использование графов
Один из способов вычислить количество кривых линий между двумя точками - это представить их в виде графа. Каждая кривая линия будет представлена в виде ребра графа, а каждая точка - в виде вершины графа. Количество кривых линий между двумя точками равно количеству путей между соответствующими вершинами графа. Вы можете использовать различные алгоритмы поиска путей, такие как алгоритм поиска в ширину или алгоритм Дейкстры, для подсчета количества путей.
Способ 2: Использование формулы комбинаторики
Еще один способ вычислить количество кривых линий между двумя точками - использовать формулу комбинаторики. Количество кривых линий можно рассматривать как количество комбинаций точек на плоскости, через которые проходит кривая линия. Формула комбинаторики для вычисления этого количества выглядит следующим образом:
C = (n-1)!
Где n - количество точек, через которые проходит кривая линия. Вы можете использовать эту формулу, зная количество точек, чтобы вычислить количество кривых линий между двумя точками.
Способ 3: Использование геометрических преобразований
Еще один способ вычислить количество кривых линий между двумя точками - использовать геометрические преобразования. Вы можете применить геометрические преобразования для перемещения исходных точек в другие положения, где вычисление количества кривых линий станет проще. Затем вы можете использовать стандартные методы подсчета количества кривых линий в новом положении точек.
Обратите внимание, что эти методы зависят от конкретной задачи и предполагают определенные условия. Некоторые задачи могут иметь более сложные подходы и требовать использования дополнительных знаний и вычислительных методов.
Математический подход к определению количества кривых линий
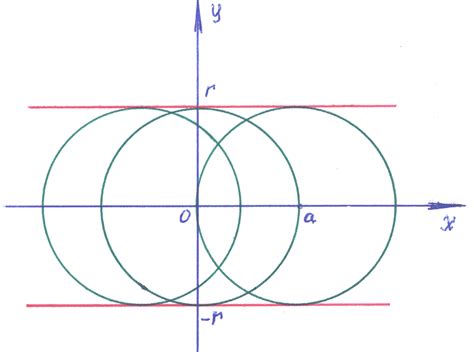
Один из таких подходов - это использование геометрических фигур и теории графов. Для определения количества кривых линий между двумя точками можно рассмотреть все возможные пути, которые соединяют эти точки, и отметить их на графике. Каждая кривая линия будет представлять собой отдельный путь. Далее, можно использовать различные алгоритмы графов, такие как алгоритм Дейкстры или поиск в глубину, чтобы выяснить количество кривых линий, соединяющих две заданных точки.
Другой подход - это использование аналитической геометрии и уравнения прямых или кривых. Каждая кривая линия может быть представлена математическим уравнением. Например, для линейных кривых можно использовать уравнение прямой, а для кривых второго порядка - уравнение эллипса, гиперболы или параболы. Затем, можно установить условия, при которых уравнения принимают одно и то же значение в двух заданных точках, и найти количество решений для этих условий. Количество решений будет соответствовать количеству кривых линий.
Таким образом, математический подход к определению количества кривых линий между двумя точками представляет собой комбинацию использования геометрических фигур, теории графов и аналитической геометрии. Выбор подхода зависит от конкретной задачи и области применения.
Физическая интерпретация количества кривых линий
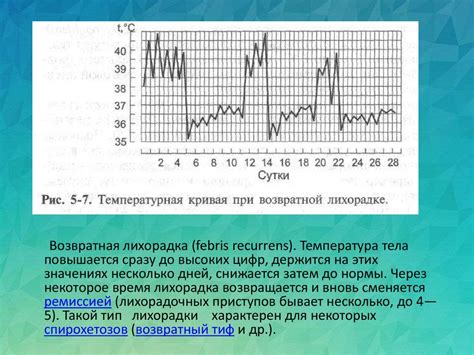
Количество кривых линий между двумя точками может иметь физическую интерпретацию в различных областях науки и инженерии.
В механике и физике количество кривых линий может указывать на различные механизмы движения объектов. Например, в газовой динамике количество кривых линий между двумя точками может отображать потоки газа или жидкости. Чем больше кривых линий, тем сильнее поток.
В электромагнетизме количество кривых линий может описывать линии силового поля, магнитного потока или электрического тока. Чем больше кривых линий, тем сильнее поле или поток.
Также количество кривых линий может быть связано с плотностью энергии или силы в пространстве. Чем больше кривых линий, тем выше плотность энергии или силы в заданной точке.
Интерпретация количества кривых линий может отличаться в разных областях науки и инженерии, но в целом они позволяют графически визуализировать и анализировать различные физические явления.
Графическое представление количества кривых линий
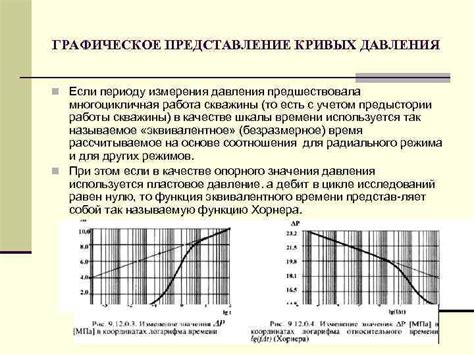
Количество кривых линий между двумя точками может быть визуализировано с помощью графического представления. Это позволяет наглядно представить взаимосвязь между точками и определить, сколько линий может быть проведено.
Один из способов графического представления количества кривых линий - это использование диаграммы, где каждая линия представляет собой отдельную связь между точками. Для каждой кривой линии может быть использован различный стиль, чтобы отличать их друг от друга.
Второй способ - использование визуализации с использованием геометрических фигур. Например, каждая кривая линия может быть представлена в виде окружности, эллипса, спирали и т.д. Такое представление позволяет наглядно показать форму и направление каждой линии.
Третий способ - использование графа, где каждая точка представляет собой узел, а кривые линии - это ребра, соединяющие узлы. Это позволяет визуально представить сложные системы связей между точками и определить количество линий между ними.
Графическое представление количества кривых линий помогает визуализировать данные и делает их более понятными. Оно может быть полезным в различных областях, таких как математика, физика, компьютерная графика и другие, где имеется необходимость в анализе и визуализации связей между объектами.
Количество кривых линий и их влияние на образование геометрических фигур

Когда речь идет о связи между двумя точками, количество кривых линий, которые могут быть проведены, играет важную роль в формировании геометрических фигур. Каждая кривая линия имеет свои особенности и влияет на образование определенной формы.
Начнем с простейшей кривой линии - прямой. Прямая линия представляет собой самую прямую траекторию между двумя точками и она имеет минимальное влияние на формирование геометрических фигур. При движении от одной точки к другой по прямой линии, мы получаем простую соединительную линию, которая не образует углов и не создает сложных форм.
Более интересными формами становятся кривые линии, такие как окружность и эллипс. Окружность создается при движении по плавной кривой, равной расстоянию от центра окружности до любой точки на ее окружности. Окружность является красивой и симметричной формой, и она может быть использована для создания множества геометрических фигур, таких как круг, диск и многоугольник с равносторонними сторонами.
Эллипс имеет похожую форму, но его кривая линия имеет более овальную форму. Эллипс создается при движении по плавной кривой, сумма расстояний от которой до двух фокусов постоянна. Эллипс также может быть использован для создания разнообразных геометрических фигур, например, овала и многоугольника с неравными сторонами.
Кривые линии также влияют на образование сложных форм, таких как спираль и зигзаг. Спираль формуется при повороте относительно центральной точки и одновременном увеличении расстояния до нее. Зигзаг создается при движении по зигзагообразной кривой, описываемой чередующимися прямыми и косыми сегментами.
Таким образом, количество и тип кривых линий, которые могут быть проведены между двумя точками, определяют форму геометрической фигуры. Каждая кривая линия обладает своими особенностями и создает уникальные фигуры, от простых прямых линий до сложных спиралей и зигзагов.
Примеры расчета количества кривых линий
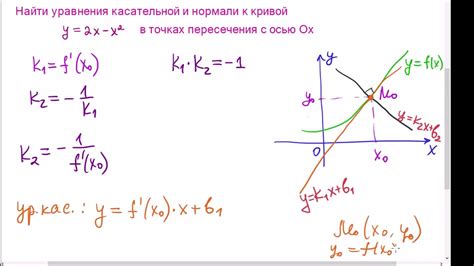
Расчет количества кривых линий между двумя точками может быть полезен при анализе геометрических объектов или при проектировании сетей связи. В данном разделе мы рассмотрим несколько примеров расчета количества кривых линий по различным алгоритмам.
Пример 1: Расчет количества кривых линий между двумя точками на плоскости.
Допустим, у нас есть две точки A(x1, y1) и B(x2, y2) на плоскости. Для расчета количества кривых линий между этими точками можно воспользоваться формулой длины отрезка:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Где d - длина отрезка между точками A и B.
Пример 2: Расчет количества кривых линий между двумя точками в трехмерном пространстве.
Если точки A и B заданы в трехмерном пространстве, то для расчета количества кривых линий можно использовать формулу расстояния между точками в трехмерном пространстве:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
Где d - расстояние между точками A и B.
Пример 3: Расчет количества кривых линий между двумя точками на сфере.
Если точки A и B заданы на сфере, то для расчета количества кривых линий можно использовать формулу длины большого круга между точками на сфере:
d = R * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))
Где d - длина большого круга между точками A и B на сфере, R - радиус сферы, lat1, lat2 - широты точек A и B, lon1, lon2 - долготы точек A и B.
Это лишь некоторые примеры алгоритмов расчета количества кривых линий между двумя точками. В каждом конкретном случае необходимо использовать соответствующую формулу в зависимости от размерности пространства, на котором заданы точки. Однако, общая задача сводится к определению расстояния или длины между этими точками.
Практическое применение количества кривых линий
Количество кривых линий между двумя точками на плоскости может иметь различные практические применения в разных сферах деятельности. Ниже приведены несколько примеров:
| Сфера применения | Примеры |
|---|---|
| Картография | При разработке карт и планов, количество кривых линий между двумя точками может быть использовано для определения сложности маршрута или для показа географической структуры местности. Таким образом, картографы могут использовать это количество в качестве визуальной информации для обозначения определенных участков или объектов на карте. |
| Транспорт и логистика | В сфере транспорта и логистики, знание количества кривых линий между двумя точками может быть полезным для определения оптимального маршрута или для оценки времени доставки груза. Это данные могут быть использованы для планирования маршрутов транспортных средств или определения наиболее эффективных путей доставки. |
| Компьютерная графика | В компьютерной графике, количество кривых линий может использоваться для создания различных эффектов и анимаций. Например, при создании анимации движения объектов на экране, количество кривых линий может влиять на плавность и естественность движения. |
1. Количество кривых линий может служить показателем сложности или связности связей между точками. Чем больше линий, тем более сложная структура и взаимосвязи присутствуют между элементами.
2. При малом количестве кривых линий информация может быть недостаточно наглядной и не передавать все взаимосвязи между точками. В этом случае возможно необходимо использовать дополнительные способы визуализации данных.
3. Слишком большое количество кривых линий может привести к перегрузке информацией и усложнению восприятия. При этом важно находить баланс между понятностью и точностью передачи данных.
4. Количество кривых линий также может иметь эстетическое значение. Оптимальное количество линий может создавать визуально привлекательное и гармоничное впечатление.
Итак, при работе с визуализацией данных важно учитывать количество кривых линий между точками, чтобы достичь оптимального сочетания наглядности, понятности и эстетической привлекательности.



