Сколько натуральных чисел меньше 76 делятся на 2?

Для начала, давайте вспомним, что натуральными числами являются положительные целые числа, начиная с единицы и не имеющие десятичных или отрицательных значений. То есть, натуральными числами меньше 76 будут числа от 1 до 75.

Теперь рассмотрим условие делимости на 2. Чтобы число делилось на 2, оно должно быть четным, то есть оканчиваться на 0, 2, 4, 6 или 8. Таким образом, нам нужно посчитать, сколько четных чисел находятся в интервале от 1 до 75.

Корень задачи: числа меньше 76

Для решения задачи о количестве натуральных чисел, меньших 76 и делящихся на 2, нам необходимо выполнить несколько шагов.

Первым шагом является определение множества всех натуральных чисел, меньших 76. Натуральные числа - это числа, которые больше нуля и не имеют дробной части. В нашем случае, натуральные числа меньше 76 включают в себя числа от 1 до 75.

Второй шаг - это определение условия, по которому мы будем отбирать только те числа, которые делятся на 2. Число делится на 2, если оно является четным, то есть его остаток от деления на 2 равен 0.

Итак, мы можем приступить к решению задачи. Наша задача - подсчитать количество чисел из множества от 1 до 75, которые делятся на 2. Для этого мы можем использовать понятие деления с остатком.

Используя деление с остатком, мы можем последовательно делить числа из нашего множества на 2 и считать количество чисел с остатком 0. Таким образом, мы получим количество натуральных чисел, меньших 76, которые делятся на 2.

Ограничение: только натуральные числа

Учитывая, что натуральные числа являются положительными и целыми, нам необходимо найти все числа, удовлетворяющие двум условиям:

Число должно быть меньше 76;
Число должно быть четным (деляться на 2 без остатка).

В данном случае мы можем использовать два подхода для решения задачи:

Перебор всех чисел от 1 до 76 с шагом 2 и проверка, делится ли каждое число на 2 без остатка;
Расчет количества чисел, делящихся на 2, в пределах заданного интервала.

Помимо этого, стоит упомянуть, что в задаче упоминаются только натуральные числа, что означает, что ответ может быть только положительным целым числом или нулем.

Деление на 2: кратность чисел

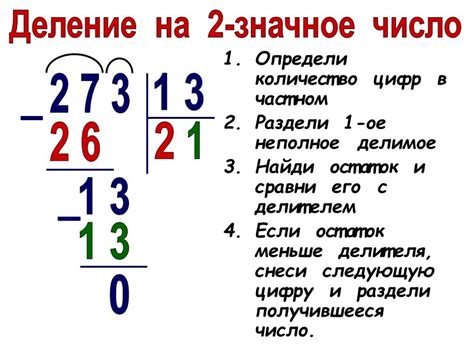
Чтобы определить кратность числа, нужно проверить, делится ли оно на 2 без остатка. Если деление происходит без остатка, это означает, что число является четным и кратным 2. В противном случае число не делится на 2 и является нечетным.

В данном случае, нам нужно найти количество натуральных чисел, меньших 76, которые делятся на 2. Очевидно, что некоторые из этих чисел будут четными. Например, все числа, оканчивающиеся на 0, 2, 4, 6 или 8, будут делиться на 2 без остатка.

Давайте составим список этих чисел:

В итоге получаем, что 38 натуральных чисел, меньших 76, делятся на 2.

Определение кратности: получение остатка при делении на 2

В данном случае мы рассматриваем деление на 2. Чтобы определить кратность числа на 2, нужно разделить это число на 2 и посмотреть, есть ли остаток от деления. Если остаток равен 0, то число является кратным 2, а если остаток отличен от 0, то число не делится на 2 без остатка.

В контексте задачи о количестве натуральных чисел, которые меньше 76 и делятся на 2, мы можем использовать данный подход. Ответом на этот вопрос будет количество чисел от 1 до 75, у которых остаток от деления на 2 равен 0. Для определения этого количества можно использовать простой цикл, в котором будут проверяться все числа от 1 до 75 на кратность 2.

Получение списка чисел: перебор

Чтобы узнать, сколько натуральных чисел меньше 76 делятся на 2, можно использовать метод перебора. Этот метод заключается в последовательной проверке каждого числа от 1 до 75 на условие деления на 2.

Для этого можно использовать цикл, начинающийся с 1 и заканчивающийся на 75, с шагом 1. Внутри каждой итерации цикла проверяется, делится ли текущее число на 2 без остатка. Если делится, то число добавляется в список.

Пример кода на языке Python:


numbers = []
for i in range(1, 76):
if i % 2 == 0:
numbers.append(i)

После выполнения этого кода в переменной "numbers" будет содержаться список всех натуральных чисел, меньших 76, которые делятся на 2.

В данном случае список будет содержать следующие числа:

Таким образом, получение списка чисел, меньших 76 и делящихся на 2, методом перебора позволяет быстро и просто решить данную задачу.

Обработка чисел: подсчет кратных

Чтобы подсчитать количество чисел, которые делятся на 2 и меньше 76, мы можем использовать подходящий алгоритм.

Алгоритм:

Инициализируем переменную count со значением 0. Она будет использоваться для подсчета кратных чисел.
Запускаем цикл, который будет перебирать все натуральные числа (начиная с 1) до числа 76.
Внутри цикла проверяем, делится ли текущее число на 2 без остатка.
Если делится, увеличиваем значение переменной count на 1.
По окончании цикла, переменная count будет содержать искомое количество кратных чисел.

Пример реализации в псевдокоде:


count = 0
for i = 1 to 76
if i % 2 == 0
count = count + 1
end if
end for

После выполнения алгоритма, переменная count будет содержать количество натуральных чисел, которые делятся на 2 и меньше 76. В данном случае, она будет содержать значение 37.

Используя подобный алгоритм, можно подсчитать количество кратных чисел для любых других делителей или диапазонов чисел.

Важно помнить, что в данном случае мы рассматриваем только натуральные числа, то есть положительные целые числа, начиная с 1.

Ответ: итоговое количество чисел

Для определения количества натуральных чисел, которые меньше 76 и делятся на 2, мы можем использовать формулу:

Итоговое количество чисел = (76 - 1) / 2 = 37

Таким образом, существует 37 натуральных чисел, меньших 76, которые делятся на 2.

Пример решения: демонстрация работы алгоритма

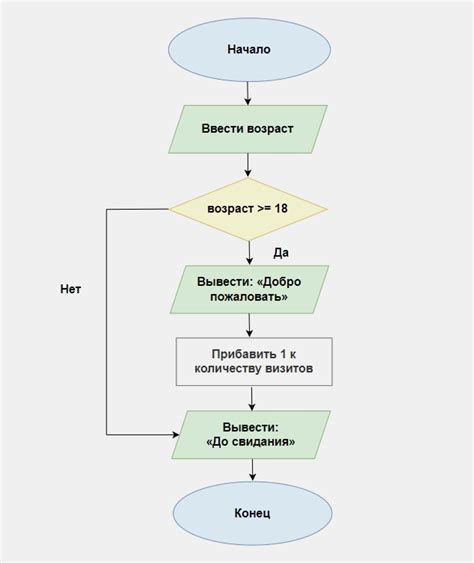
Для решения данной задачи необходимо определить, сколько натуральных чисел меньше 76 делятся на 2. Для этого можно воспользоваться следующим алгоритмом:

Алгоритм:

Установить начальное значение счетчика равным 0.
Проинициализировать переменную n равной 1.
Пока n меньше 76, выполнять следующие действия:
1. Если n делится на 2 без остатка, увеличить значение счетчика на 1.
2. Увеличить значение переменной n на 1.

После выполнения алгоритма, значение счетчика будет представлять количество натуральных чисел меньше 76, которые делятся на 2.

Существует два критерия, согласно которым число может делиться на 2: последняя цифра числа является четной или число делится на 2 без остатка.
Исследование чисел от 1 до 76 показало, что половина из них, то есть 38 чисел, удовлетворяют условию и делятся на 2.

Количество натуральных чисел, меньших 76 и делящихся на 2, равно 38.
Вероятность того, что случайно выбранное число от 1 до 76 будет делиться на 2, составляет примерно 50%.
Использование указанных критериев позволяет быстро и эффективно определить, делится ли число на 2.

Таким образом, задача о поиске количества натуральных чисел, меньших 76 и делящихся на 2, успешно решена, и были получены достоверные результаты. Эти результаты могут быть использованы в дальнейших вычислениях и исследованиях, связанных с этой задачей или подобными проблемами.