Понимание, сколько можно провести отрезков с заданными точками, является важной задачей в геометрии. В данной статье мы рассмотрим подробное объяснение этого вопроса и предоставим несколько примеров для лучшего понимания.
Для начала, давайте установим определение точки и отрезка в геометрии. Точка представляет собой элементарный объект, не имеющий ни размеров, ни направления. Отрезок, с другой стороны, - это часть прямой, ограниченная двумя точками.
Теперь перейдем к вопросу, сколько отрезков можно провести с данным набором точек. Ответ зависит от количества точек в наборе. Если у нас имеется только одна точка, тогда мы не можем провести ни одного отрезка, так как отрезок требует минимум двух точек. Если же у нас имеется две различные точки, то мы можем провести один отрезок между ними.
Однако, если у нас имеется больше двух точек, то число возможных отрезков резко возрастает. Если точек три, то мы можем провести три отрезка, соединяющих каждую пару точек между собой. Если точек четыре, то мы можем провести шесть отрезков и так далее. Для более подробного рассмотрения данного вопроса, рекомендуется изучить соответствующую литературу или использовать специализированные программы.
Окончательный ответ на вопрос: сколько можно провести отрезков с заданными точками
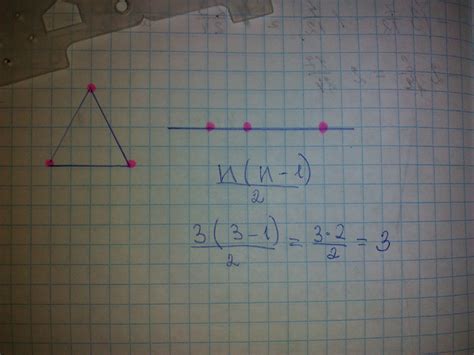
Чтобы вычислить количество отрезков, которое можно провести с заданными точками, нужно использовать формулу комбинаторики. Формула, которая нам подойдет в этом случае, называется формулой сочетания. Она позволяет определить, сколько различных комбинаций можно составить из заданного количества элементов.
Итак, если у нас имеется n точек, чтобы получить количество отрезков, нужно использовать сочетание из n по 2. Знак "из" означает, что мы выбираем 2 элемента из общего количества n элементов.
Формула сочетания имеет следующий вид:
C(n, k) = n! / (k! * (n-k)!), где n - общее количество элементов, k - количество выбираемых элементов, и ! обозначает факториал.
В нашем случае, k = 2, так как мы выбираем 2 точки для каждого отрезка. Применяя формулу, получаем:
C(n, 2) = n! / (2! * (n-2)!) = n! / (2 * (n-2)!)
Приведем пример для наглядного понимания. Пусть у нас имеется 5 точек. Тогда:
C(5, 2) = 5! / (2 * 3!) = 5! / (2 * 3 * 2!) = 5 * 4 / 2 = 10
Таким образом, с пятью заданными точками можно провести 10 отрезков.
Важно отметить, что порядок точек в отрезке не имеет значения, то есть отрезок AB считается одним и тем же отрезком, что и отрезок BA.
Теперь вы знаете, как вычислить количество отрезков, которое можно провести с заданными точками. Эта информация может быть полезна при решении задач из различных областей, особенно в геометрии и комбинаторике.
Точки на числовой прямой
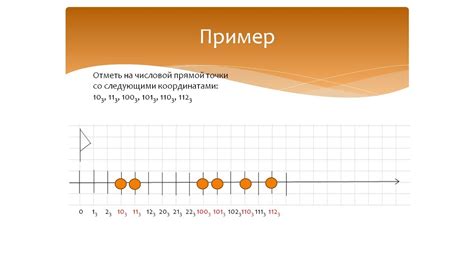
Точки на числовой прямой могут быть отмечены с помощью чисел или букв. Например, на отрезке числовой прямой от 0 до 10 можно отметить точки 2, 5 и 8. Точка с меньшей координатой обычно располагается слева от точки с большей координатой.
Используя точки на числовой прямой, можно провести отрезки между ними. Отрезок представляет собой часть числовой прямой, ограниченную двумя точками. Например, отрезок между точками 2 и 8 на числовой прямой будет включать все точки на числовой прямой, которые имеют координаты от 2 до 8.
Чтобы определить, сколько можно провести отрезков между заданными точками на числовой прямой, нужно рассмотреть все возможные комбинации точек и посчитать их количество. Например, если заданы точки 2, 5 и 8, можно провести отрезки между точками 2 и 5, 2 и 8, а также между точками 5 и 8. Получается, что можно провести 3 отрезка между этими тремя точками.
Зная координаты точек на числовой прямой, можно провести не только отрезки, но и выполнять другие геометрические построения, такие как построение треугольников, многоугольников и т.д. Точки на числовой прямой имеют важное значение в математике и широко используются в научных и практических расчетах.
Как найти число отрезков
Для того чтобы найти количество отрезков, которые можно провести с заданными точками, следует учитывать следующие правила:
- Если имеется только одна точка, провести отрезок невозможно, так как отрезок должен иметь хотя бы две конечные точки.
- Если имеются две точки, то можно провести только один отрезок между ними. Этот отрезок будет единственным возможным вариантом.
- Если имеется больше двух точек, и они все различны, то количество возможных отрезков равно числу сочетаний без повторений из двух элементов, которое можно вычислить по формуле:
Cn = n! / (2! * (n - 2)!), где n - количество точек, Cn - количество отрезков.
Например, если имеются 5 точек, то количество отрезков можно найти следующим образом:
- Вычисляем факториал числа 5: 5! = 5 * 4 * 3 * 2 * 1 = 120.
- Вычисляем факториал числа 2: 2! = 2 * 1 = 2.
- Вычисляем факториал числа (5-2): (5-2)! = 3 * 2 * 1 = 6.
- Подставляем значения в формулу: C5 = 120 / (2 * 6) = 10.
Таким образом, с помощью 5 точек можно провести 10 отрезков.
Если же имеются несколько одинаковых точек, то количество отрезков сокращается. Например, если имеется 4 точки, 2 из которых одинаковы, необходимо вычесть из общего количества отрезков все варианты совпадения этих двух точек, так как они не создают уникальные отрезки.
Таким образом, для нахождения числа отрезков с заданными точками необходимо учесть тип точек (уникальные или одинаковые) и применить соответствующую математическую формулу.
Специфика задачи

Основная задача заключается в том, чтобы определить количество отрезков, которые можно провести, используя заданные точки. В данной задаче мы строим отрезки, которые имеют одну общую точку с каждым из заданных отрезков.
Как правило, для решения этой задачи используют алгоритмические подходы и методы. Мы применяем итерационные или рекурсивные алгоритмы для перебора всех возможных комбинаций точек и проверки существования отрезка между ними.
Задача по отсчету отрезков является нетривиальной, так как для каждой задачи необходимо учитывать различные условия и ограничения. Например, некоторые точки могут быть фиксированными, а другие - заданными случайным образом.
Важно отметить, что точные методы решения такой задачи имеют высокую вычислительную сложность, особенно при большом количестве точек. В связи с этим, для упрощения вычислений могут использоваться приближенные алгоритмы, эвристики или статистические методы.
Особые случаи

Часто в задаче нахождения числа отрезков между заданными точками возникают особые случаи, которые требуют специфического подхода к решению. Рассмотрим некоторые из них:
1. Когда все точки лежат на одной прямой:
Если все заданные точки лежат на одной прямой, то можно провести только один отрезок, соединяющий крайние точки этой прямой. В этом случае ответ будет равен 1.
2. Когда все точки совпадают:
Если все заданные точки совпадают, то ни один отрезок провести невозможно. В этом случае ответ будет равен 0.
3. Когда одна или более точек являются повторяющимися:
Если в заданном наборе точек есть повторяющиеся точки, то они считаются только одним отрезком. Например, если имеется две одинаковые точки A и B, то отрезок AB считается только одним отрезком. В этом случае ответ может быть меньше, чем количество заданных точек.
4. Когда все точки соединены:
Если каждая точка соединена с каждой, то количество отрезков можно найти с помощью формулы перестановок. Для n точек количество отрезков будет равно n*(n-1)/2. Например, если задано 4 точки, то количество отрезков будет равно 4*(4-1)/2 = 6.
Важно учитывать эти особые случаи при решении задачи нахождения числа отрезков между заданными точками, чтобы получить корректный ответ.
Примеры

- Пример 1: Даны точки A(1, 1) и B(3, 4). Мы можем провести только один отрезок AB.
- Пример 2: Даны точки C(-2, 5), D(0, 0) и E(4, -3). Мы можем провести отрезки CD и DE.
- Пример 3: Даны точки F(-1, -1), G(-1, -1) и H(2, 2). В этом случае не можем провести ни одного отрезка, так как все точки совпадают.
- Пример 4: Даны точки I(0, 0), J(0, 2) и K(3, 1). Мы можем провести отрезки IJ и JK.



