Один из основных вопросов, связанных с геометрией, заключается в том, сколько отрезков образуется при пересечении двух отрезков. Эта задача имеет широкое применение в различных областях, включая математику, физику, информатику и даже искусство.
Пересечение двух отрезков может представлять собой различные ситуации. Если отрезки пересекаются внутри одного из них, то образуется два отрезка: один находится слева от пересечения, а другой - справа. Если же отрезки пересекаются только в одной точке, то можно считать, что образуется один отрезок, который имеет общую точку пересечения с исходными отрезками.
Если отрезки пересекаются на протяжении нескольких точек, то количество образующихся отрезков будет зависеть от их расположения и взаимного отношения. В этом случае может образоваться как один большой отрезок, охватывающий все точки пересечения, так и несколько отрезков, которые имеют общие точки пересечения, но не охватывают все.
Интересующие моменты

- Отрезки могут пересекаться в различных точках, создавая различные конфигурации.
- Если отрезки пересекаются в одной точке, то образуется один отрезок, состоящий из этой точки.
- Если отрезки параллельны и имеют одинаковую длину, то они совпадают.
- Если отрезки имеют общую точку пересечения, но не пересекаются полностью, то образуется два отрезка.
- Если отрезок полностью содержится внутри другого отрезка, то он не является пересекающимся.
- Количество пересекающихся отрезков зависит от их конфигурации и может быть любым числом от одного до бесконечности.
Как отрезки пересекаются
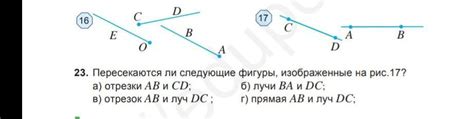
При пересечении двух отрезков может произойти несколько сценариев:
| Сценарий | Описание |
|---|---|
| Пересечение внутри | Отрезки пересекаются внутри одного из них, при этом могут совпадать или быть частично равными |
| Пересечение по концам | Один из концов одного отрезка лежит на другом отрезке, при этом отрезки не пересекаются внутри |
| Отрезки равны | Оба отрезка полностью совпадают между собой |
| Отрезки параллельны и не пересекаются | Отрезки не имеют общих точек и лежат на параллельных прямых |
В каждом из этих случаев количество отрезков остается неизменным, так как пересечение двух отрезков не приводит к созданию новых отрезков. Однако, в зависимости от сценария пересечения могут быть выделены разные области на графике.
Как определить количество отрезков
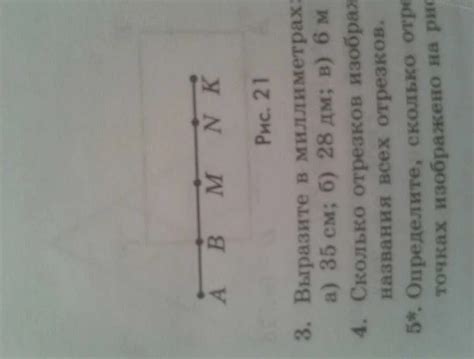
Количество отрезков, образованных пересечением двух отрезков, может быть разным в зависимости от их взаимного расположения.
Если два отрезка не пересекаются, то количество отрезков равно двум.
Если два отрезка пересекаются внутри друг друга, то количество отрезков также равно двум.
Если два отрезка пересекаются только в одной точке, то количество отрезков равно трем.
Если два отрезка пересекаются по одной прямой, то количество отрезков будет бесконечным.
Исходя из этого, для определения количества отрезков необходимо проанализировать взаимное расположение отрезков.
Пример: Пересекающиеся отрезки AB и CD имеют следующее количество отрезков:
1. Если AB и CD не пересекаются - два отрезка
2. Если AB и CD пересекаются внутри друг друга - два отрезка
3. Если AB и CD пересекаются только в одной точке - три отрезка
4. Если AB и CD пересекаются по одной прямой - бесконечное количество отрезков
Таким образом, для определения количества отрезков необходимо учитывать место их пересечения.
Математические примеры

- Пример 1: Если два отрезка пересекаются точечно, то общее количество отрезков не изменится и останется равным двум.
- Пример 2: Если два отрезка пересекаются посередине, то каждый отрезок разделится на две части, и общее количество отрезков увеличится на единицу.
- Пример 3: Если два отрезка пересекаются под прямым углом, то создаются 4 новых отрезка, образующих прямоугольник.
- Пример 4: Если два отрезка пересекаются под острым углом, то общее количество отрезков увеличится, но точное количество зависит от угла пересечения и длины отрезков.
- Пример 5: Если два отрезка параллельны и находятся на одной прямой, то они не будут пересекаться и останутся двумя отдельными отрезками.
Практическое применение

Знание количества отрезков, полученных при пересечении двух отрезков, имеет практическую значимость во многих областях:
Это лишь некоторые примеры практического применения знания о количестве отрезков, полученных при их пересечении. Данное понятие широко используется в различных областях и помогает решать конкретные задачи, связанные с геометрией, анализом и моделированием объектов. |
Задачи по данной теме

Решение задач по пересечению отрезков помогает лучше понять и применить теоретические знания в практических ситуациях. Вот некоторые задачи, которые могут помочь закрепить материал:
| Номер задачи | Описание |
|---|---|
| 1 | Дано два отрезка на числовой оси. Найти их пересечение, если оно существует. |
| 2 | Пользователь задает координаты четырех точек - концов двух отрезков. Определить, пересекаются ли эти отрезки. |
| 3 | Пользователь вводит координаты четырех точек - концов двух отрезков. Найти координаты точек пересечения, если они существуют, или вывести сообщение о их отсутствии. |
| 4 | Дано несколько отрезков. Определить, сколько пар отрезков пересекаются. |
| 5 | Пользователь вводит координаты концов двух отрезков. Определить, пересекаются ли они и построить их графическое представление. |
Решение этих задач поможет лучше понять особенности работы с отрезками, а также научиться применять полученные знания в реальных задачах.
Важность понимания этой концепции

Эта концепция основывается на объективных математических законах и правилах, которые позволяют точно определить количество отрезков, образующихся в результате пересечения двух других отрезков. Это позволяет ученым и инженерам проводить точные расчеты и предсказания, которые основываются на математической точности.
Понимание этой концепции также имеет практическое применение в различных областях, таких как архитектура, гражданское строительство, геодезия и даже компьютерная графика. Зная, сколько отрезков будет, если два отрезка пересекаются, специалисты могут проектировать здания, строить дороги и создавать компьютерные модели с высокой точностью и надежностью.



