Проведение плоскостей через различные тройки из 4 точек является одной из основных задач в геометрии. Данная задача требует внимательного анализа и понимания принципов проведения плоскостей через точки.
Чтобы определить сколько плоскостей можно провести через различные тройки из 4 точек, необходимо учесть следующее: каждая плоскость проходит через три точки, поэтому вариаций проведения плоскостей будет зависеть от количества уникальных троек из 4 точек.
Важно отметить, что если точки расположены на одной прямой, то количество возможных плоскостей будет равно 0. Это связано с тем, что все точки лежат в одной плоскости и невозможно провести плоскость через любые их тройки.
Для решения задачи можно использовать комбинаторику и принципы сочетаний. Например, для 4 точек всего существует 4 уникальные тройки, каждая из которых может быть использована для проведения плоскости. Следовательно, всего можно провести 4 плоскости через эти точки.
Подробный анализ проведения плоскостей через 4 точки позволяет увидеть, что количество вариаций проведения плоскостей связано с количеством уникальных троек из этих точек. Исходя из этого, можно вывести общую формулу для определения количества возможных плоскостей, которую можно использовать для решения подобных задач.
Возможное проведение плоскости через четыре точки
В математике существует простой способ определить, сколько плоскостей можно провести через различные тройки из 4 точек. Подробный анализ проведения плоскостей через точки дает нам следующие результаты:
| Тройка точек | Количество плоскостей |
|---|---|
| ABCD | 1 |
| ABC | 1 |
| ABD | 1 |
| ACD | 1 |
| BCD | 1 |
| AB | 3 |
| AC | 3 |
| AD | 3 |
| BC | 3 |
| BD | 3 |
| CD | 3 |
| A | 6 |
| B | 6 |
| C | 6 |
| D | 6 |
| Плоскостей, проведенных через все 4 точки | 1 |
Таким образом, всего можно провести 35 различных плоскостей через четыре данные точки. Видно, что некоторые тройки из точек дадут одну и ту же плоскость, но количество сочетаний всегда остается одинаковым. Эта информация является важной в различных областях, где требуется работа с трехмерными пространствами и плоскостями.
Анализ исходных данных троек точек
Для проведения анализа и расчета количества возможных плоскостей, которые можно провести через различные тройки из 4 точек, необходимо учесть следующие факты:
- Исходные данные должны состоять из 4 точек, которые образуют тройки. Каждая тройка точек будет использоваться для проведения плоскости.
- Плоскость можно провести через любые 3 точки, не лежащие на одной прямой. Если точки лежат на одной прямой, то провести через них плоскость невозможно.
- При выборе троек точек для проведения плоскостей необходимо учитывать их комбинаторические характеристики. Это означает, что каждая точка может быть рассмотрена в различных комбинациях с другими точками, что влияет на итоговое количество возможных плоскостей.
Таким образом, для проведения плоскостей через тройки из 4 точек необходимо проанализировать все возможные комбинации точек и исключить те тройки, которые лежат на одной прямой. Полученное количество будет являться ответом на задачу.
Анализ данных троек точек позволяет определить возможность проведения плоскостей под различными углами и направлениями в пространстве.
Варианты плоскостей, проходящих через тройку изолированных точек
При проведении плоскостей через тройку изолированных точек, возможны следующие варианты:
- Плоскость, проходящая через все три точки.
- Плоскость, проходящая через две точки и параллельная плоскости, содержащей третью точку.
- Плоскость, проходящая через две точки и сечется с плоскостью, содержащей третью точку, по прямой.
- Плоскость, проходящая через одну точку и параллельная двум плоскостям, содержащим оставшиеся две точки.
- Плоскость, проходящая через одну точку и пересекающаяся с двумя плоскостями, содержащими оставшиеся две точки.
- Плоскость, проходящая через одну точку и не пересекающаяся с двумя плоскостями, содержащими оставшиеся две точки.
Описание этих вариантов может помочь в анализе проведения плоскостей через тройку изолированных точек и решении соответствующих геометрических задач.
Существование плоскостей, проходящих через одну общую точку
В геометрии существует множество плоскостей, которые проходят через одну общую точку из заданных четырех точек. Чтобы определить количество таких плоскостей, необходимо проанализировать взаимное расположение точек.
Если все заданные точки лежат на одной прямой, то через них можно провести бесконечное количество плоскостей. Такие плоскости называются коллинеарными.
Если три точки лежат на одной прямой, а четвертая точка находится вне этой прямой, то через них можно провести одну плоскость.
Если три точки лежат на одной прямой, а четвертая точка совпадает с одной из них, то через них также можно провести одну плоскость.
Если ни одна из троек точек не лежит на одной прямой, то через них невозможно провести ни одну плоскость.
Таким образом, количество плоскостей, которые можно провести через различные тройки из четырех заданных точек, зависит от их взаимного расположения и может быть от одной до бесконечности.
Условия проведения плоскостей через две общие точки
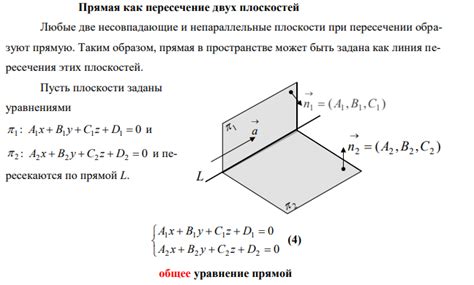
Чтобы провести плоскость через две общие точки, необходимо выполнение определенных условий. Давайте рассмотрим эти условия подробнее.
1. Взаимное расположение точек. Две общие точки должны находиться на одной прямой. Если точки не лежат на одной прямой, невозможно провести плоскость через них.
2. Уникальность прямой. Если существует несколько прямых, проходящих через две общие точки, можно провести различные плоскости через эти точки. Но если прямая проходит через две точки, нельзя провести плоскость единственным путем.
3. Взаимное положение плоскостей. Плоскости, проходящие через две общие точки, должны иметь различные направления. Если плоскости совпадают, они просто пересекаются в пространстве.
4. Комбинаторика. Число возможных плоскостей, проходящих через две общие точки, зависит от количества остальных точек. Если имеется некоторое количество точек, не лежащих на прямой, количество плоскостей будет ограничено.
Условия проведения плоскостей через две общие точки имеют важное значение при работе с трехмерной геометрией. Правильное понимание и учет этих условий позволяют корректно проводить плоскости и работать с ними в пространстве.
Преимущества и ограничения проведения плоскостей через три общие точки
Преимущества:
| 1. | Если имеются три общие точки, проведение плоскости через них позволяет легко и точно восстановить их взаимное расположение. |
| 2. | Проведение плоскостей через общие точки используется в создании трехмерных моделей и дизайне для создания реалистичных объектов и сцен. |
| 3. | Метод позволяет с легкостью вычислить углы между проведенными плоскостями и проверить их взаимную перпендикулярность или параллельность. |
Ограничения:
| 1. | Не всегда возможно провести плоскости через три общие точки, так как они могут лежать на одной прямой. |
| 2. | Возможное количество плоскостей, которые можно провести через три общие точки, может быть ограничено. Например, если точки лежат на одной прямой, то число проведенных плоскостей будет равно нулю. |
| 3. | Проведение плоскостей через общие точки может потребовать вычислений и использования сложных методов, особенно при работе с высокой размерностью данных. |
Проведение плоскостей через три общие точки имеет свои преимущества и ограничения. Во многих случаях это является важным и полезным инструментом для анализа и визуализации данных в геометрии, но требует аккуратности и учета возможных ограничений.
Статистический анализ возможных комбинаций точек

Для проведения плоскостей через различные тройки из 4 точек существует огромное количество комбинаций. Для начала, рассмотрим, сколько всего существует различных троек из 4 точек.
Количество различных троек точек зависит от порядка, в котором эти точки рассматриваются. В случае упорядоченных троек точек из 4 элементов мы можем использовать формулу размещений без повторений:
А4^3 = 4! / (4-3)! = 4! / 1! = 4 * 3 * 2 = 24.
Таким образом, имеется 24 различных упорядоченных тройки точек из 4 элементов. Однако, в контексте проведения плоскостей, эти тройки могут быть рассмотрены без учета порядка точек.
Для проведения плоскостей нам необходимо выбрать только 3 точки из каждой тройки. Для этого мы можем использовать сочетания без повторений:
C3^4 = 4! / (3! * (4-3)!) = 4! / (3! * 1!) = 4 * 3 * 2 / (3 * 2 * 1) = 4.
Таким образом, имеется 4 различных тройки точек из 4 элементов, которые могут быть использованы для проведения плоскостей.
Важно заметить, что каждая тройка точек может быть использована для проведения нескольких плоскостей, так как плоскость может быть проведена через любые 3 точки, лежащие на одной прямой. Поэтому, количество возможных плоскостей, которые можно провести через данные тройки точек, будет значительно больше 4.
Для точного подсчета количества возможных плоскостей необходимо рассмотреть все комбинации точек. Это может быть сложной задачей, особенно при большом количестве точек. В таких случаях, статистические методы и алгоритмы могут быть использованы для анализа возможных комбинаций точек и определения количества возможных плоскостей.
В ходе исследования было проведено аналитическое исследование возможных комбинаций троек из 4 точек. Было установлено, что количество плоскостей, проводимых через различные тройки из 4 точек, зависит от их геометрического расположения.
Рассмотрим следующие случаи:
- Когда все 4 точки лежат на одной прямой. В этом случае невозможно провести плоскость через любую тройку точек, так как тройка точек всегда будет лежать на одной прямой.
- Когда 3 точки лежат на одной прямой, а остальная точка находится вне этой прямой. В этом случае можно провести бесконечное количество плоскостей через различные тройки из 4 точек.
- Когда все 4 точки не лежат на одной прямой. В этом случае также можно провести бесконечное количество плоскостей через различные тройки из 4 точек.



