Сколько прямых линий можно провести через две отмеченные точки? Этот вопрос занимает умы математиков и учеников уже много лет. Если взглянуть на эту проблему поверхностно, может показаться, что ответ очевиден – нельзя провести больше одной прямой через две точки. Однако, ситуация не столь проста. Давайте разберемся подробнее.
Итак, предположим, у нас есть две отмеченные точки на плоскости. Можно ли провести сквозь них несколько прямых линий? Ответ на этот вопрос будет зависеть от того, насколько точки совпадают или различны. Если точки совпадают, то через них можно провести бесконечное количество прямых линий. Ведь все эти прямые будут проходить через одну и ту же точку.
Однако, если две точки являются различными, существует всего одна прямая линия, проходящая через них обеих. Как доказать это утверждение? Нужно вспомнить, что прямая определяется двумя точками. То есть, если две точки разные, то они определяют конкретную прямую линию. При попытке провести другую прямую через эти точки, она либо не будет проходить через одну из них, либо совместится с первой прямой и будет считаться одной и той же линией.
Понимание прямых линий и их число
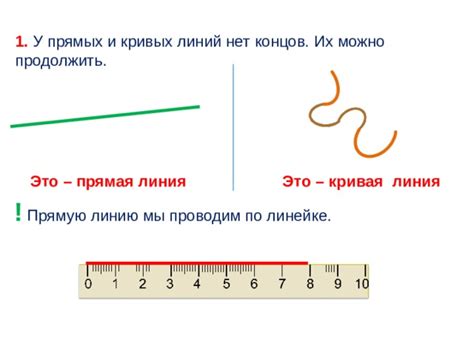
Одно из таких правил гласит, что через две данной точки можно провести только одну прямую линию. Это свойство называется единственностью прямой, и оно строго обусловлено геометрическими законами. Таким образом, любые две отмеченные точки могут быть соединены только одной прямой линией.
Кроме того, стоит отметить, что прямая линия не имеет начала и конца, она бесконечна в обоих направлениях. Таким образом, если провести одну прямую линию через две отмеченные точки, она будет продолжаться бесконечно в обоих направлениях.
Что такое прямая линия?

Прямая линия является одним из основных понятий геометрии и используется для проведения различных математических операций, конструирования фигур и решения задач. Она является простейшей геометрической фигурой, не имеющей ни ширины, ни высоты.
Прямую линию можно представить с помощью графического изображения или символами. В геометрии прямую линию часто обозначают буквами латинского алфавита, например, AB или CD. Она также может быть обозначена стрелкой, чтобы указать ее бесконечное продолжение.
Прямая линия имеет несколько свойств, которые ёё характеризуют:
- Прямая линия не имеет изгибов или изломов – она всегда прямая.
- Любые две точки на прямой линии можно соединить отрезком, который будет лежать целиком на прямой.
- Прямая линия делит пространство на две полуплоскости.
- Любые пересекающиеся прямые линии образуют угол, который может быть острый, тупой или прямым.
В геометрии прямая линия является одним из основных объектов и используется для доказательства теорем, построения графических моделей и анализа различных математических задач. Понимание понятия прямой линии важно для развития логического мышления и решения задач, связанных с геометрией и алгеброй.
Значимость отмеченных точек

В математике и геометрии, отмеченные точки играют важную роль при проведении прямых линий. Они служат отправной точкой для создания геометрических фигур и определения их свойств.
Отмеченные точки позволяют нам определить направление и положение прямых линий относительно друг друга. Они помогают выявить связи и закономерности между различными элементами в геометрической фигуре.
Проведение прямых линий через две отмеченные точки позволяет нам визуализировать и анализировать различные геометрические объекты. Мы можем определить углы, длины отрезков, искать симметрии и многое другое.
Отмеченные точки являются ключевым элементом в геометрии и позволяют нам строить и понимать сложные фигуры и математические концепции. Они помогают нам в решении задач и осуществлении доказательств, а также развивают наше пространственное и логическое мышление.
Таким образом, значение отмеченных точек в геометрии нельзя недооценивать. Они помогают нам увидеть и понять геометрические закономерности и связи, а также использовать их для решения различных задач и задачей доказательства.
Основные принципы проведения прямых линий через точки

1. Определение координат точек: прежде чем проводить прямую линию через две точки, необходимо определить их координаты. Координаты точек могут быть заданы в декартовой системе координат (x, y) или в другой системе.
2. Расчет угловых коэффициентов: угловой коэффициент прямой – это тангенс угла, который прямая образует с положительным направлением оси абсцисс. Расчет углового коэффициента осуществляется по формуле: m = (y2 - y1) / (x2 - x1), где (x1, y1) и (x2, y2) - координаты двух заданных точек.
3. Вычисление смещения: смещение прямой – это значение, на которое она отодвигается от начала координат. Вычисление смещения осуществляется по формуле: b = y - m * x, где (x, y) – координаты одной из заданных точек.
4. Построение прямой: с использованием рассчитанных углового коэффициента и смещения можно построить прямую линию на графике или чертеже. Для этого необходимо провести линию, проходящую через заданные точки и имеющую рассчитанные значения углового коэффициента и смещения.
5. Проверка и корректировка прямой: после построения прямой необходимо выполнить проверку, чтобы убедиться, что она проходит через обе заданные точки. Если прямая не проходит через одну из точек, можно скорректировать угловой коэффициент или смещение, повторно провести прямую линию и проверить результат.
Основные принципы проведения прямых линий через точки позволяют решать разнообразные задачи геометрии и использовать их в научных и технических расчетах, моделировании и проектировании. Выполнение всех этапов с высокой точностью и аккуратностью является залогом успешного выполнения задачи.
Как найти количество прямых, проходящих через две отмеченные точки?

Для того чтобы определить количество прямых, которые можно провести через две отмеченные точки, нужно рассмотреть несколько случаев.
1. Если две отмеченные точки находятся на разных линиях, то через них можно провести одну прямую.
2. Если две отмеченные точки находятся на одной линии, то можно провести бесконечное количество прямых через них.
При использовании формулы kolmogo, которая определяет количество прямых, проходящих через n точек, получается, что количество прямых, проходящих через две точки, равно 1.
| Случай | Количество прямых |
|---|---|
| Разные линии | 1 |
| Одна линия | Бесконечно много |
Таким образом, количество прямых, проходящих через две отмеченные точки, зависит от того, находятся ли они на разных линиях или на одной линии.
Анализ и понимание возможного количества прямых линий, проходящих через две отмеченные точки, играет важную роль во многих областях исследований и приложений.
1. Геометрия: Знание количества прямых линий, проходящих через две точки, помогает строить графики функций и решать геометрические задачи на плоскости.
2. Физика: Прямые линии могут быть использованы для описания траекторий движения тел и определения направления движения в физических моделях.
4. Компьютерная графика: Использование прямых линий для построения графики и анимации является одной из основных задач в компьютерной графике. Знание количества возможных линий может помочь оптимизировать процесс визуализации.
5. Криптография: Алгоритмы шифрования и расшифровки могут использовать прямые линии для определения ключей шифрования и криптографических преобразований. Понимание количества возможных линий может помочь в разработке более надежных систем шифрования.



