Многоугольники - это фигуры, у которых есть много сторон и углов. Одним из интересных вопросов, которые можно задать о многоугольниках, является вопрос о количестве их сторон. Существует формула, позволяющая вычислить количество сторон многоугольника, зная сумму его углов.
Итак, давайте решим задачу. Для начала, нам необходимо знать, что сумма углов многоугольника равна (n-2) * 180 градусов, где n - количество сторон многоугольника. По условию задачи, сумма углов равна 1080 градусов. Подставим эту величину в формулу и решим уравнение: (n-2) * 180 = 1080.
Раскроем скобки и упростим уравнение: n * 180 - 2 * 180 = 1080.
Теперь, проведя несложные математические операции, получим: n * 180 - 360 = 1080.
Добавим 360 к обеим сторонам уравнения: n * 180 = 1440.
Наконец, разделим обе стороны уравнения на 180: n = 1440 / 180.
Подсчитав значение, мы обнаружим, что многоугольник имеет n = 8 сторон.
Многоугольник: определение и свойства

Многоугольники могут быть выпуклыми или невыпуклыми. В случае выпуклого многоугольника все углы между сторонами многоугольника будут острыми. В невыпуклом же многоугольнике найдутся углы, которые будут тупыми или прямыми.
У многоугольника есть несколько свойств, которые можно использовать для его характеризации:
- Сумма всех внутренних углов многоугольника равна (n-2)*180 градусам, где n - количество сторон многоугольника.
- Все внутренние углы многоугольника могут быть разделены на (n-2) треугольника.
- Сумма длин всех сторон многоугольника называется его периметром.
- Многоугольник с n сторонами называется n-угольником.
Зная эти свойства, мы можем определить, что многоугольник с суммой углов 1080 является шестиугольником.
Сумма углов многоугольника
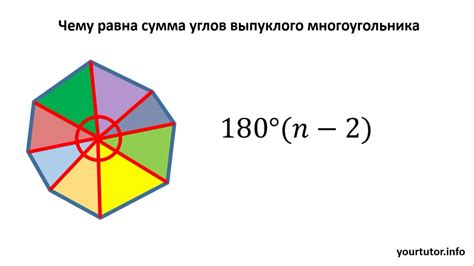
Сумма углов многоугольника зависит от количества его сторон. Для нахождения суммы углов многоугольника с n сторонами, используется формула: (n-2) * 180.
Например, для треугольника (n=3) сумма углов будет равна (3-2) * 180 = 180 градусов. Для четырехугольника (n=4) сумма углов будет равна (4-2) * 180 = 360 градусов. И так далее.
Если известна сумма углов многоугольника, то можно определить количество его сторон. Для этого используется формула: n = (сумма углов / 180) + 2.
Например, если сумма углов многоугольника равна 1080 градусов, то количество его сторон будет равно (1080 / 180) + 2 = 8.
Таким образом, многоугольник с суммой углов 1080 будет иметь 8 сторон.
Сколько сторон у многоугольника?

Дано, что сумма углов многоугольника составляет 1080 градусов. Подставим это значение в формулу и найдем количество сторон:
180*(n-2) = 1080
n-2 = 6
n = 8
Таким образом, многоугольник с суммой углов 1080 имеет 8 сторон.
Общая формула

Для нахождения количества сторон многоугольника с заданной суммой углов можно использовать следующую формулу:
Количество сторон = (Сумма углов - 360) / 180
Эта формула основана на том, что в многоугольнике сумма всех внутренних углов равна 180 * (Количество сторон - 2).
Найдя разность между суммой заданных углов и 360 (что соответствует одной дополнительной оборотной стороне), мы можем разделить эту разность на 180, чтобы найти количество дополнительных сторон.
Таким образом, если сумма заданных углов равна 1080, можно использовать формулу:
Количество сторон = (1080 - 360) / 180 = 720 / 180 = 4
То есть многоугольник с суммой углов 1080 будет иметь 4 стороны.
Как найти число сторон?

Чтобы найти число сторон многоугольника, имея информацию о сумме его углов, можно воспользоваться формулой:
| Число сторон | Сумма углов |
|---|---|
| 3 | 180° |
| 4 | 360° |
| 5 | 540° |
| 6 | 720° |
| 7 | 900° |
| 8 | 1080° |
| ... | ... |
Продолжая эту последовательность, можно установить, что многоугольник с суммой углов 1080° имеет 8 сторон. Таким образом, ответ на вопрос составляет 8.
Пример поиска числа сторон

Предположим, у нас есть многоугольник с неизвестным числом сторон и суммой углов равной 1080. Чтобы найти число сторон многоугольника, мы можем использовать формулу суммы углов многоугольника:
Сумма углов многоугольника = (n-2) * 180 градусов, где n - число сторон многоугольника.
Подставим известные данные в формулу:
1080 = (n-2) * 180
Решим уравнение:
1080 = 180n - 360
Добавим 360 к обеим частям уравнения:
1440 = 180n
Разделим обе части уравнения на 180:
n = 8
Таким образом, многоугольник с суммой углов 1080 имеет 8 сторон.
Сколько сторон у многоугольника с суммой углов 1080?

Для вычисления количества сторон многоугольника, при сумме углов 1080 градусов, мы можем использовать следующее равенство: (n-2) * 180 = 1080.
Перейдем к решению уравнения:
n - 2 = 1080 / 180
n - 2 = 6
n = 6 + 2
n = 8
Таким образом, многоугольник с суммой углов 1080 имеет 8 сторон.



