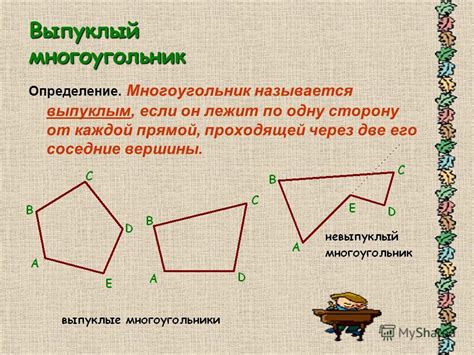
Выпуклый многоугольник – это фигура, у которой все внутренние углы меньше 180 градусов. Углы многоугольников являются важным свойством, которое обуславливает их форму и количество сторон. Однако, зная сумму углов многоугольника, можно выяснить, сколько он имеет сторон.
Для выпуклых многоугольников существует формула, которая позволяет определить количество сторон по сумме углов. Сумма углов выпуклого многоугольника равна 180 градусам умноженным на количество сторон минус два: S = (180 * n) - 360, где S – сумма углов, n – количество сторон.
Таким образом, чтобы найти количество сторон выпуклого многоугольника с суммой углов 2520, мы можем воспользоваться данной формулой. Заменив S на 2520, мы получим уравнение 2520 = (180 * n) - 360. Решив его, мы найдем, сколько сторон имеет данный многоугольник.
Выпуклый многоугольник: определение и свойства

Определение выпуклого многоугольника основывается на свойствах его углов. Все углы выпуклого многоугольника являются острыми, то есть меньше 180 градусов. Кроме того, сумма всех его углов должна быть равной 180 градусов умноженных на количество его сторон минус два.
Для примера, рассмотрим выпуклый многоугольник с суммой углов 2520 градусов. Известно, что сумма всех углов многоугольника равна 180 градусов умноженных на количество его сторон минус два. Значит, для данного многоугольника:
180 * n - 360 = 2520, где n - количество сторон многоугольника.
Приведя уравнение к упрощенному виду, получаем:
180 * n = 2880,
n = 16.
Таким образом, выпуклый многоугольник с суммой углов 2520 градусов имеет 16 сторон.
Выпуклые многоугольники обладают рядом других свойств. Например, они не имеют самопересечений, то есть их стороны не пересекаются друг с другом. Кроме того, выпуклый многоугольник всегда можно построить на плоскости, если известны координаты его вершин.
Выпуклые многоугольники широко применяются в геометрии и вычислительной геометрии для решения различных задач, таких как вычисление площади или определение наличия пересечений между ними.
Определение выпуклого многоугольника
У выпуклого многоугольника также есть следующие свойства:
- Все его стороны представляют собой отрезки прямых.
- Все его углы между сторонами лежат в пределах от 0 до 180 градусов.
- Любая линия, соединяющая две точки на многоугольнике, полностью лежит внутри или на границе этого многоугольника.
- Замкнутая ломаная, образованная его сторонами, не пересекает себя.
Степень выпуклого многоугольника равна сумме его внутренних углов. По теореме, степень многоугольника равна (n-2)*180 градусов, где n - количество вершин многоугольника. В случае, когда степень многоугольника равна 2520 градусам, требуется найти количество его сторон.
Свойства выпуклых многоугольников
Вот несколько свойств выпуклых многоугольников:
- Углы: Сумма всех внутренних углов выпуклого многоугольника с n сторонами равна (n-2) * 180 градусов.
- Углы: Каждый угол выпуклого многоугольника меньше 180 градусов.
- Стороны: Количество сторон выпуклого многоугольника равно количеству его вершин.
- Диагонали: В выпуклом многоугольнике с n сторонами существует (n * (n-3)) / 2 диагоналей.
- Вершины: Сумма всех внутренних углов, образуемых вершинами выпуклого многоугольника, равна 360 градусов.
- Периметр: Периметр выпуклого многоугольника равен сумме длин всех его сторон.
- Площадь: Площадь выпуклого многоугольника можно вычислить с помощью формулы Гаусса: Площадь = полусумма всех векторных произведений его сторон и их определенных векторов.
Зная эти свойства, можно решать различные задачи, связанные с выпуклыми многоугольниками, например, находить их периметр, площадь, проверять условия на выпуклость и т.д.
Сумма углов в выпуклом многоугольнике

В данном случае, если сумма углов в многоугольнике равна 2520 градусов, то у нас есть уравнение:
| Сумма углов | = | (n-2) * 180 |
|---|---|---|
| 2520 | = | (n-2) * 180 |
Решая уравнение, получаем:
| 2520 | = | n * 180 - 360 | ||
|---|---|---|---|---|
| 2520 | + | 360 | = | n * 180 |
| 2880 | = | n * 180 |
Делая обратный расчет, получаем:
| n | = | 2880 / 180 |
|---|---|---|
| n | = | 16 |
Таким образом, выпуклый многоугольник с суммой углов 2520 имеет 16 сторон.
Формула для расчета суммы углов в многоугольнике

Сумма углов в выпуклом многоугольнике может быть вычислена с помощью следующей формулы:
S = (n - 2) * 180°
где S - сумма углов многоугольника, а n - количество сторон многоугольника.
В данной задаче нам известна сумма углов многоугольника (2520°), поэтому мы можем использовать данную формулу для определения количества сторон многоугольника:
S = (n - 2) * 180°
2520° = (n - 2) * 180°
Решив уравнение, мы найдем количество сторон многоугольника, которое составляет n.
Таким образом, выпуклый многоугольник с суммой углов 2520° имеет n сторон.
Пример: выпуклый многоугольник с суммой углов 2520
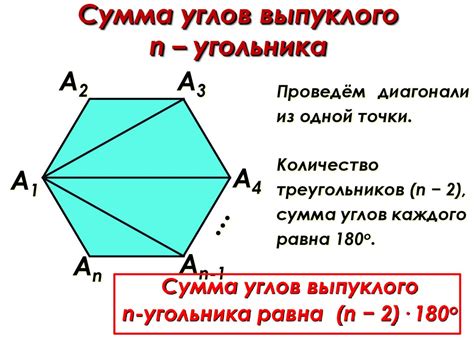
Выпуклый многоугольник это фигура, у которой все углы меньше 180 градусов и все точки, лежащие на прямой между двумя любыми точками фигуры, также лежат внутри или на границе этой фигуры.
Сумма всех внутренних углов выпуклого многоугольника вычисляется по формуле: S = (n - 2) * 180, где n - количество сторон многоугольника.
Для нахождения количества сторон выпуклого многоугольника с заданной суммой углов воспользуемся формулой и подставим в нее значение 2520:
S = (n - 2) * 180
2520 = (n - 2) * 180
2520/180 = n - 2
14 = n - 2
n = 16
Таким образом, выпуклый многоугольник с суммой углов 2520 имеет 16 сторон.
Определение числа сторон
Для определения числа сторон в выпуклом многоугольнике с суммой углов 2520 необходимо рассмотреть свойство суммы внутренних углов.
Выпуклый многоугольник имеет внутренние углы, сумма которых равна (n - 2) * 180°, где n - число сторон многоугольника.
Подставляя известные значения в формулу, получаем уравнение:
- (n - 2) * 180° = 2520°
Разрешая уравнение относительно n, получаем:
- n - 2 = 2520° / 180°
- n - 2 = 14
- n = 16
Таким образом, данный выпуклый многоугольник имеет 16 сторон.
Связь числа сторон с суммой углов в многоугольнике
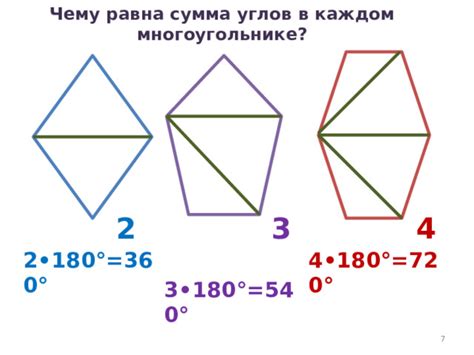
Сумма углов в многоугольнике – это сумма всех внутренних углов, измеряемых в градусах.
Существует связь между числом сторон и суммой углов в многоугольнике. Известно, что для любого выпуклого многоугольника с числом сторон n сумма всех его внутренних углов равна (n - 2) * 180 градусов.
Таким образом, для заданной суммы углов можно найти количество сторон выпуклого многоугольника, применив формулу:
n = (сумма углов / 180) + 2
Например, если сумма углов в многоугольнике равна 2520 градусов, то количество сторон можно найти следующим образом:
n = (2520 / 180) + 2 = 16
Таким образом, выпуклый многоугольник с суммой углов 2520 градусов имеет 16 сторон.
Нахождение числа сторон для многоугольника с суммой углов 2520
Пусть у нас есть выпуклый многоугольник. Мы знаем, что сумма всех его углов равна 2520. Как найти число сторон этого многоугольника?
Для начала, давайте вспомним формулу для суммы углов внутри любого многоугольника: (n-2) * 180, где n - число сторон многоугольника. Согласно этой формуле, сумма углов внутри n-угольника равна (n-2) * 180.
Мы знаем, что сумма углов равна 2520, поэтому:
(n-2) * 180 = 2520
Раскроем скобки и упростим уравнение:
n * 180 - 2 * 180 = 2520
n * 180 = 2520 + 360
n * 180 = 2880
Теперь делим обе части уравнения на 180:
n = 2880 / 180
n = 16
Таким образом, получаем, что выпуклый многоугольник с суммой углов 2520 имеет 16 сторон.



