Четверичная система счисления – это система счисления, в которой используется четыре различных цифры: 0, 1, 2 и 3. В отличие от десятичной системы, где каждая позиция имеет значение, увеличивающееся в 10 раз по сравнению с предыдущей, в четверичной системе каждая позиция увеличивается в 4 раза.
Интересно, какое количество трехзначных чисел можно представить в четверичной системе счисления? Для ответа на этот вопрос нам необходимо учесть следующее: первая цифра числа не может быть нулем, так как тогда это уже будет двузначное число. Таким образом, первую цифру можно выбрать из трех вариантов: 1, 2 или 3.
После выбора первой цифры возможными вариантами для второй и третьей цифр являются все четыре цифры: 0, 1, 2 и 3. Таким образом, количество трехзначных чисел в четверичной системе счисления равно произведению количества вариантов для каждой позиции. В данном случае, это будет равно 3 * 4 * 4 = 48.
Числа в четверичной системе счисления
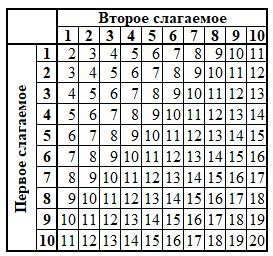
Например, число 103 в четверичной системе счисления представляет собой число, которое раскладывается следующим образом: 1 * 4^2 + 0 * 4^1 + 3 * 4^0. Таким образом, 103 в четверичной системе равно 27 в десятичной системе счисления.
Количество трехзначных чисел в четверичной системе счисления можно рассчитать, учитывая диапазон значений, которые могут принимать цифры в каждой позиции числа. Так как система счисления состоит из четырех цифр, то количество трехзначных чисел можно найти, умножив количество возможных значений в каждой из трех позиций.
В первой позиции число может принимать значения от 1 до 3, так как ноль не может быть первой значащей цифрой. Таким образом, количество возможных значений в первой позиции равно 3.
Во второй и третьей позициях число может принимать любое из четырех возможных значений. Таким образом, количество возможных значений во второй и третьей позициях также равно 4.
Таким образом, общее количество трехзначных чисел в четверичной системе счисления можно рассчитать, умножив количество возможных значений в каждой позиции: 3 * 4 * 4 = 48.
Итак, в четверичной системе счисления существует 48 трехзначных чисел.
Что такое четверичная система счисления
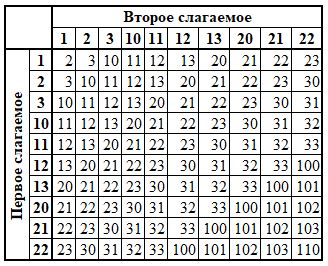
Четверичная система использует четыре символа: 0, 1, 2 и 3. Эти символы представляют количество единиц (1), двоек (2) и троек (3) в заданном числе. Каждая цифра в числе имеет свое значение, определяемое ее позицией в числе.
Например, число 103 в четверичной системе означает 1 тройку, 0 двоек и 3 единицы. Это число можно рассчитать, умножив каждую цифру на 4 в степени соответствующей позиции и сложив результаты. В данном случае: 1 * 4^2 + 0 * 4^1 + 3 * 4^0 = 16 + 0 + 3 = 19.
Четверичная система счисления часто используется в информатике и в качестве альтернативы двоичной системе счисления. Она может быть полезна при представлении и обработке данных, которые могут быть естественно организованы в группы по четыре.
Как представить трехзначные числа в четверичной системе
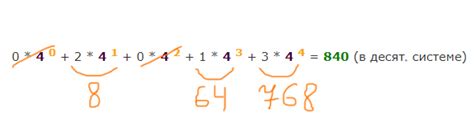
Четверичная система счисления основана на использовании четырех цифр: 0, 1, 2 и 3. В этой системе, трехзначные числа представляются с использованием трех цифр, где каждая цифра может быть любой из четырех возможных.
Для того чтобы представить трехзначное число в четверичной системе, мы используем позиционную систему счисления. Каждая цифра числа имеет вес, который определяет ее место в числе. В трехзначных числах вес каждой цифры увеличивается справа налево: сотни, десятки и единицы.
Например, число 423 в четверичной системе представляется следующим образом:
4 - это количество сотен (4 * 4^2 = 64)
2 - это количество десятков (2 * 4^1 = 8)
3 - это количество единиц (3 * 4^0 = 3)
Суммируя веса каждой цифры, мы получаем значение числа в десятичной системе: 64 + 8 + 3 = 75. Таким образом, число 423 в четверичной системе эквивалентно числу 75 в десятичной системе.
Таким образом, представление трехзначных чисел в четверичной системе счисления основывается на позиционной системе счисления и весах каждой цифры. Это позволяет нам удобно работать с числами в четверичной системе и выполнять математические операции.
Сколько трехзначных чисел можно представить в четверичной системе

Четверичная система счисления основана на использовании четырех цифр: 0, 1, 2 и 3. В этой системе каждая цифра представляет определенную степень числа 4.
Для того чтобы вычислить количество трехзначных чисел, которые можно представить в четверичной системе, нужно понять, какие числа используются в трехзначных числах и сколько комбинаций можно составить из этих чисел.
В трехзначных числах каждая позиция принимает одну из четырех возможных цифр. Первая позиция может быть заполнена любой из четырех цифр (0, 1, 2 или 3), вторая позиция может быть заполнена так же и любой из четырех цифр, и так далее.
Таким образом, для первой позиции мы имеем 4 варианта, для второй позиции также 4 варианта, и для третьей позиции снова 4 варианта. По правилу перемножения, общее количество трехзначных чисел в четверичной системе равно 4 x 4 x 4 = 64.
То есть, в четверичной системе счисления можно представить 64 трехзначных числа.
Примеры трехзначных чисел в четверичной системе

Четверичная система счисления состоит из четырех цифр: 0, 1, 2 и 3. В этой системе счисления трехзначные числа представляются как комбинации из этих четырех цифр.
Ниже приведены некоторые примеры трехзначных чисел в четверичной системе:
| Десятичное число | Четверичное число |
|---|---|
| 0 | 00 |
| 1 | 01 |
| 2 | 02 |
| 3 | 03 |
| 4 | 10 |
| 5 | 11 |
| 6 | 12 |
| 7 | 13 |
| 8 | 20 |
| 9 | 21 |
| 10 | 22 |
| 11 | 23 |
| 12 | 30 |
| 13 | 31 |
| 14 | 32 |
| 15 | 33 |
И так далее. Количество трехзначных чисел в четверичной системе равно 64. Каждое число имеет уникальное представление в этой системе, которое может быть использовано для математических операций или преобразований.



