Вопрос о том, какое число является самым большим, занимает умы историков, математиков и философов на протяжении веков. Ответ на него может казаться простым - число, которое больше всех остальных. Однако реальность оказывается не такой простой.
Поиск наибольшего числа рассматривается в различных областях, начиная со школьной программы математики и заканчивая сложными научными исследованиями. В математике существуют различные методы и алгоритмы для нахождения максимального числа, которые основываются на сравнении чисел с помощью математических операций.
Наибольшее число может быть найдено с помощью метода перебора, когда все возможные числа сравниваются между собой. Однако этот подход является крайне неэффективным при больших объемах данных. В научных исследованиях применяются более сложные алгоритмы, такие как сортировка или поиск максимума в массиве данных, что позволяет найти самое большое число быстрее и эффективнее.
Однако поиск наибольшего числа может быть не только математической задачей, но и объектом философских рассуждений. Философы задаются вопросами о природе числа, его бесконечности и ограниченности. Они исследуют взаимосвязь чисел с другими аспектами реальности и пытаются понять, можно ли найти абсолютное наибольшее число, которое будет превосходить все остальные числа.
Что такое число?

Число - это абстрактный математический объект, который используется для измерения, счета и расчетов. Числа могут иметь различное значение и свойства, и они широко применяются в нашей повседневной жизни.
Числа могут быть представлены различными способами: целыми числами (положительными и отрицательными), десятичными дробями, десятичными числами с плавающей запятой, рациональными числами (заданными отношением двух целых чисел) или иррациональными числами (числами, которые не могут быть представлены в виде дроби).
Числа используются во многих областях, включая физику, экономику, технику, информатику и другие науки. Они также являются основой для проведения математических операций, таких как сложение, вычитание, умножение и деление.
В математике существует бесконечное количество чисел, и они могут быть классифицированы по различным критериям. Например, числа могут быть натуральными, целыми, рациональными, иррациональными, простыми и составными. Каждый тип чисел имеет свои особенности и свойства.
Числа также используются для решения различных задач и уравнений. Например, они могут быть использованы для нахождения корней квадратного уравнения, для решения систем линейных уравнений или для проведения статистического анализа данных.
Кроме того, числа могут иметь различное значение в разных контекстах. Например, в физике числа могут представлять физические величины, такие как время, расстояние или скорость. В экономике числа могут представлять денежные суммы или процентные ставки.
Таким образом, число - это важный и неотъемлемый элемент нашей жизни и математики в целом. Оно позволяет нам измерять, считать и проводить различные расчеты, а также решать задачи и уравнения в различных областях знаний.
Математические операции с числами
Математические операции с числами - это основные действия, которые можно выполнять с числами для получения новых значений. В основе таких операций лежит арифметика, которая позволяет складывать, вычитать, умножать и делить числа.
Приведем основные математические операции:
- Сложение - операция, при которой два числа объединяются в одно число путем их суммирования. Символ сложения (+) используется для обозначения этой операции. Пример: 2 + 3 = 5
- Вычитание - операция, при которой из одного числа вычитается другое число и получается результат. Символ вычитания (-) используется для обозначения этой операции. Пример: 5 - 2 = 3
- Умножение - операция, при которой одно число умножается на другое число и получается результат. Символ умножения (*) используется для обозначения этой операции. Пример: 2 * 3 = 6
- Деление - операция, при которой одно число делится на другое число и получается результат. Символ деления (/) используется для обозначения этой операции. Пример: 6 / 3 = 2
Кроме основных операций, существуют и другие математические операции, такие как возведение в степень, извлечение корня, нахождение остатка от деления и другие. Однако в данном обзоре мы не будем останавливаться на этих операциях.
Математические операции с числами являются основой для решения различных математических задач, а также они широко используются в повседневной жизни, например, для подсчета цен, расчета скидок, учета денежных средств и многих других ситуациях.
Разные виды чисел
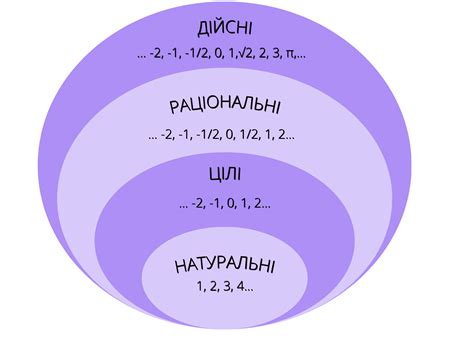
В мире существуют разные виды чисел, каждое из которых имеет свои особенности и свойства. Рассмотрим некоторые из них:
Натуральные числа - это числа, которые используются для обозначения количества элементов в конечных множествах. Натуральные числа начинаются с единицы (1) и продолжаются до бесконечности. Примеры натуральных чисел: 1, 2, 3, 4, 5 и т.д.
Целые числа - это числа, которые включают в себя натуральные числа, их отрицания и нуль. Целые числа можно представить как точки на числовой прямой. Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3 и т.д.
Рациональные числа - это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа включают в себя как конечные, так и периодические десятичные дроби. Примеры рациональных чисел: 1/2, 0.25, -3/4, 2.333 и т.д.
Иррациональные числа - это числа, которые не могут быть представлены в виде дроби. Иррациональные числа имеют бесконечную и непериодическую десятичную запись. Примеры иррациональных чисел: √2 (корень квадратный из 2), π (число Пи), е (основание натурального логарифма) и т.д.
Действительные числа - это числа, которые включают в себя как рациональные, так и иррациональные числа. Действительные числа можно представить в виде точек на числовой прямой. Примеры действительных чисел: -3, 0, 1, √2, π и т.д.
Существуют и другие виды чисел, такие как комплексные числа, которые используются в математике и физике, но мы не будем рассматривать их подробно в этом обзоре.
Изучение разных видов чисел позволяет более глубоко понять мир математики и его приложения в реальной жизни. Каждый вид чисел имеет свои особенности и применение, что делает их все важными и интересными.
Как определить самое большое число?
Определение самого большого числа может быть важным для решения различных задач. В этом разделе мы рассмотрим несколько способов определения наибольшего числа.
Метод сравнения
Простейший способ определить самое большое число - сравнить их друг с другом. Для этого нам понадобится использовать операторы сравнения, такие как больше (>), меньше (<) и равно (==).
1. Сравниваем два числа: а и б.
- Если а больше б, то а является самым большим числом.
- Если а меньше б, то б является самым большим числом.
- Если а равно б, то и а, и б являются самыми большими числами.
2. Если у нас есть больше двух чисел, мы можем использовать ту же логику для каждой пары чисел, сравнивая их и находя самое большое число.
Метод сортировки
Другой способ определить самое большое число - это отсортировать числа по убыванию и взять первое число из отсортированного списка.
1. Создадим список из чисел, которые мы хотим отсортировать.
2. Отсортируем числа по убыванию - от самого большого к самому маленькому.
3. Возьмем первое число из отсортированного списка. Это и будет самое большое число.
Например, если у нас есть список чисел [5, 2, 9, 1, 7], после сортировки мы получим [9, 7, 5, 2, 1], и самое большое число будет 9.
Метод поиска максимального числа
Еще один способ определить самое большое число - это использовать специальную функцию поиска максимального числа. Во многих языках программирования есть встроенные функции или методы, которые могут найти максимальное число из заданного списка.
1. Создадим список из чисел, которые мы хотим проверить.
2. Используем функцию поиска максимального числа для нахождения самого большого числа в списке.
3. Полученное максимальное число будет самым большим числом.
Например, в Python мы можем использовать функцию max() для нахождения самого большого числа:
numbers = [5, 2, 9, 1, 7]
max_number = max(numbers)
print(max_number) (результат: 9)
Заключение
В данном разделе мы рассмотрели несколько способов определить самое большое число. Вы можете выбрать подходящий метод в зависимости от конкретной задачи или языка программирования, которым вы пользуетесь. Важно помнить, что для определения наибольшего числа нужно учитывать контекст и требования задачи.
Примеры самых больших чисел в разных областях

Числа - это неотъемлемая часть математики и науки в целом. В разных областях знания существуют самые большие числа, которые играют важную роль в различных расчетах и моделях. Рассмотрим несколько примеров самых больших чисел.
Число Авогадро
Одно из наиболее известных больших чисел - число Авогадро (6.022 × 10^23). Оно используется в химии и физике для определения количества частиц вещества в молях. Число Авогадро представляет собой количество атомов, молекул или других частиц в одном моле вещества. Это число играет важную роль в различных расчетах и химических уравнениях.
Гуголплекс
Гуголплекс (10^(10^100)) - это одно из самых больших чисел, которое невозможно точно представить или записать. Оно превышает количество атомов в наблюдаемой вселенной. Гуголплекс используется в теории информации и математике для описания огромных числовых значения и вычислительных сложностей.
Сконцентрированный индекс Грама-Смита
В математике существуют числа, которые используются для измерения сложности алгоритмов и анализа эффективности вычислений. Сконцентрированный индекс Грама-Смита (92.8×10^121) является одним из самых больших известных чисел в этой области. Оно используется для измерения сложности алгоритмов и определения количества операций, которые требуются для выполнения вычислений.
Айхенмайер
Айхенмайер (10^(10^10^34)) - это огромное число, которое было введено в математической теории множеств. Оно превосходит даже гуголплекс и обозначает количество сочетаний подмножеств заданного множества. Айхенмайер используется в теории множеств, комбинаторике и теории вероятностей для изучения различных свойств и комбинаторных структур.
Это лишь несколько примеров самых больших чисел в различных областях. Математика и наука постоянно стремятся находить новые числа и устанавливать их свойства. Большие числа играют важную роль в расчетах, моделях и теориях, помогая нам лучше понять мир вокруг нас.
Что делать, если число не влезает в тип данных?
Иногда возникает ситуация, когда число, с которым мы работаем, слишком большое и не влезает в тип данных, которым мы пользуемся. Например, если мы используем целочисленный тип данных с ограниченным диапазоном значений, то число может превышать этот диапазон. В таких случаях необходимо применить специальные стратегии для работы с такими большими числами.
Одной из возможных стратегий является использование больших чисел или длинной арифметики (BigNumber или BigInteger). В этом случае мы пользуемся специальными классами или библиотеками, которые позволяют работать с числами, не ограниченными по размеру. Такие классы или библиотеки позволяют выполнять все арифметические операции с большими числами и имеют встроенные функции для работы с ними.
Еще одной стратегией может быть использование дробных чисел или чисел с плавающей точкой. Если число слишком большое для целочисленного типа данных, но при этом целостность данных не является критической, то мы можем использовать тип данных с плавающей точкой. В таком случае, мы теряем точность на последних разрядах числа, но можем работать с большими числами.
Также можно использовать формат с плавающей точкой с фиксированной запятой (fixed-point). В этом формате мы используем фиксированное количество разрядов после запятой и сдвигаем запятую влево или вправо в зависимости от величины числа. Такой формат позволяет работать с большими и маленькими числами, не теряя точность в пределах заданного количества разрядов после запятой.
Иногда можно воспользоваться специальными алгоритмами или методами, которые позволяют разбить число на более мелкие блоки и работать с ними по отдельности. Например, если нам нужно выполнить сложение или умножение больших чисел, то мы можем разбить их на блоки и выполнять операции над этими блоками по очереди. Такой подход позволяет работать с числами, не превышающими лимиты типа данных.
В любом случае, выбор стратегии зависит от конкретной задачи и требований к точности и производительности. Важно учитывать, что использование более сложных стратегий может повлиять на производительность программы и потребление ресурсов. Поэтому необходимо внимательно анализировать требования и выбирать наиболее подходящий подход.
Вопрос-ответ
Какое число считается самым большим?
Самым большим числом считается число, которое превышает все остальные числа. В математике нет конечного самого большого числа, так как можно всегда добавить единицу и получить число, которое будет больше. Однако, в разных задачах и контекстах может быть определенное число, которое считается самым большим.
Каким образом определяется самое большое число в последовательности?
Для определения самого большого числа в последовательности необходимо сравнить все числа между собой и найти то, которое будет больше всех остальных. Это можно сделать путем пошагового сравнения чисел или с помощью математических операторов больше и меньше.
Может ли самое большое число быть отрицательным?
Да, самое большое число может быть отрицательным. В математике больше и меньше относительные понятия, и они могут применяться как к положительным, так и к отрицательным числам. Например, если у нас есть последовательность отрицательных чисел, самым большим числом будет число с наименьшим по модулю отрицательным значением.
Приведите пример нахождения самого большого числа в задаче.
Например, рассмотрим задачу о нахождении самого большого числа из трех чисел: 5, 9 и 3. Для этого сравниваем числа между собой: 5 < 9, 5 < 3, 9 > 3. Получаем, что самое большое число - 9.