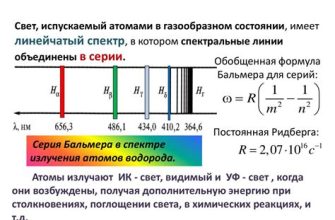
Перемещение точки является одним из фундаментальных понятий в физике и математике. Когда точка движется, ее положение в пространстве изменяется со временем. Определить, как именно точка перемещается и где она находится в конкретный момент времени, поможет знание ее пути и положения.
Путь точки - это маршрут, который она проходит от одной точки к другой. Он может быть прямым или кривым, и важно понимать, как точка перемещается по этому пути. Например, если точка движется по прямой линии, ее путь будет простым и прямым. Однако, если точка движется по кривой, ее путь может быть более сложным и изогнутым.
Положение точки - это ее местоположение в пространстве в конкретный момент времени. Определить положение точки можно с помощью системы координат, где каждая точка имеет свои координаты. Например, если точка движется по плоскости, ее положение можно определить с помощью координат x и y. Если точка движется в трехмерном пространстве, ее положение можно определить с помощью координат x, y и z.
Как перемещается точка за 6 секунд
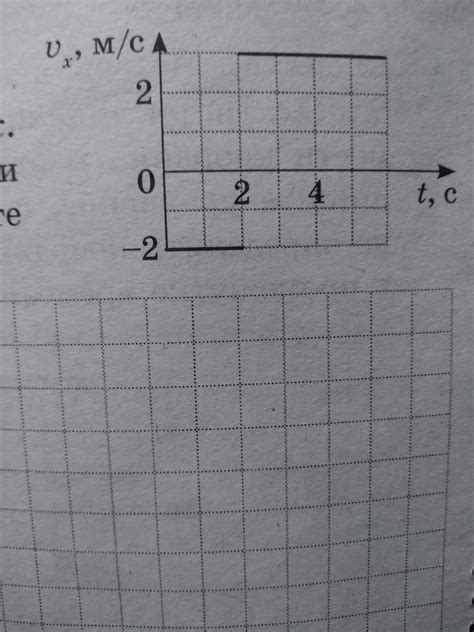
Когда точка перемещается за 6 секунд, ее движение может быть описано с использованием понятий пути и положения.
Путь точки:
Путь точки - это маршрут, который она проходит от начального положения до конечного положения. Он измеряется в единицах длины, таких как метры или километры.
Время, за которое точка перемещается, также важно для вычисления пути. Если точка перемещается со скоростью v метров в секунду, то путь можно вычислить по формуле: путь = скорость x время.
Положение точки:
Положение точки - это конкретная точка в пространстве, где находится объект в определенный момент времени. Оно может быть описано с помощью координат, например, x и y.
Для определения положения точки в пространстве, могут быть использованы различные системы координат, такие как декартова система координат (x, y), полярная система координат (r, θ) и другие.
Изменение положения точки со временем может быть описано с помощью движения в пространстве, такого как прямолинейное движение или вращение.
Пример:
Допустим, у нас есть точка, которая перемещается со скоростью 2 метра в секунду в течение 6 секунд. Значит, путь точки можно вычислить по формуле: путь = скорость x время = 2 м/с x 6 с = 12 м.
Таким образом, за 6 секунд точка переместится на расстояние 12 метров.
Чтобы определить положение точки, нам нужно знать ее начальные координаты. Пусть начальные координаты точки равны (0, 0) в декартовой системе координат. Тогда положение точки после 6 секунд можно определить, зная путь и используя формулы для прямолинейного движения или изменения положения.
Выводящийся текст выше не имеет никаких оформлений, он состоит только из последовательности абзацев и списков.
Путь и положение точки
Путь - это векторная величина, которая определяет перемещение точки относительно начальной позиции. В физике путь обозначается символом s. Путь может быть прямым или криволинейным.
Положение точки - это координаты точки в пространстве. В физике положение точки определяется с помощью координатных осей. Обычно используются декартовы координаты, где положение точки задается значениями по осям x и y. В трехмерном пространстве используется третья ось z.
Для определения пути и положения точки за 6 секунд необходимо знать скорость и направление движения точки. Скорость - это векторная величина, которая определяет изменение положения точки в единицу времени. Направление движения точки задается углом.
Определение пути и положения точки происходит с помощью соответствующих формул и законов физики, таких как закон движения прямолинейно равноускоренного движения или закон сохранения импульса.
Зная скорость и направление движения точки, можно определить ее путь и положение за 6 секунд. Для этого необходимо умножить скорость на время, чтобы получить путь, и сложить координаты начальной позиции и пути, чтобы получить конечное положение точки.
Например, если у нас есть точка, которая движется со скоростью 10 м/с в направлении угла 30 градусов относительно положительного направления оси x и находится в начальной позиции (0, 0), то через 6 секунд путь точки будет равен 60 метрам, а ее положение будет (60 * cos(30), 60 * sin(30)), то есть примерно (51.96, 30).
Таким образом, для определения пути и положения точки за 6 секунд необходимо знать скорость и направление движения точки, а также использовать соответствующие формулы и законы физики.
Начальное положение точки
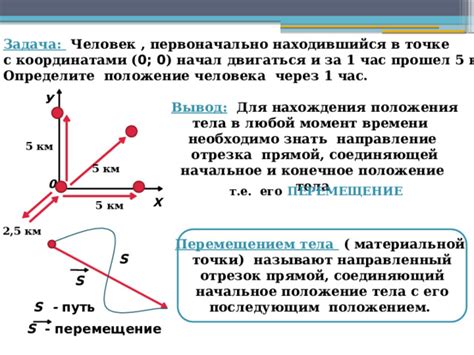
- Для определения начального положения точки можно использовать координатную систему.
- В двумерной координатной системе начальное положение точки задается двумя координатами - x и y.
- X-координата определяет расстояние до точки по горизонтали.
- Y-координата определяет расстояние до точки по вертикали.
- Обозначение начального положения точки в координатной системе выглядит как (x, y), где x - значение по оси X, y - значение по оси Y.
Определение начальной координаты
Для определения начальной координаты точки, перемещающейся за 6 секунд, необходимо иметь информацию о ее скорости и направлении движения. Если эта информация известна, можно рассчитать начальное положение точки.
- Если точка движется с постоянной скоростью по прямой линии, начальная координата может быть определена путем умножения скорости на время движения. Например, если точка движется со скоростью 10 метров в секунду, начальная координата будет равна 10 метров * 6 секунд = 60 метров.
- Если точка движется по кривой траектории, определение начальной координаты может быть сложнее. В этом случае требуется знание уравнения траектории и способов его решения для определения начальной координаты.
Если информация о скорости и направлении движения точки неизвестна, возможно использование дополнительных средств и методов, таких как технические средства определения координат (например, глобальная система позиционирования – GPS).
Итак, для определения начальной координаты точки, перемещающейся за 6 секунд, необходимо знать ее скорость и направление движения. В простых случаях можно воспользоваться формулой V * t = S, где V – скорость, t – время, S – путь, чтобы рассчитать начальную координату. В более сложных случаях возможно использование уравнений траектории и дополнительных средств определения координат.
Фиксация точки на плоскости
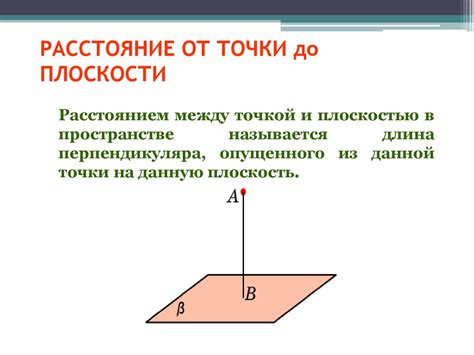
Для того чтобы зафиксировать точку на плоскости, необходимо задать ее координаты. Координаты точки обычно задаются в декартовой системе координат с помощью двух чисел – абсциссы и ординаты.
Абсцисса точки – это ее координата по оси X. Ордината точки – это ее координата по оси Y. Точка на плоскости задается парой чисел (x, y), где x – абсцисса точки, а y – ордината точки.
Для удобства восприятия координат точек на плоскости часто используется координатная сетка, которая делит плоскость на квадратные ячейки. Каждая ячейка имеет свои координаты, которые задаются с помощью целых чисел. Изначально начало координат устанавливается в центре плоскости и имеет координаты (0, 0).
Для более удобной фиксации точки на плоскости можно использовать специальные обозначения. Например, точку можно обозначить буквой P и указать ее координаты в скобках: P(2, 3). Это означает, что абсцисса точки равна 2, а ордината точки равна 3.
Если точка перемещается по плоскости, ее координаты могут меняться. Для отслеживания перемещения точки можно использовать различные методы, например, строить график ее координат или записывать изменения в таблицу.
Таким образом, фиксация точки на плоскости позволяет точно определить ее положение и отслеживать ее перемещение в пространстве. Это основной инструмент в геометрии и других науках, где требуется работа с координатами на плоскости.
Направление движения точки
Направление движения точки определяется вектором скорости. Вектор скорости - это величина, которая указывает путь и скорость движения точки.
Вектор скорости имеет две характеристики: направление и модуль. Направление вектора скорости указывает, в каком направлении движется точка. Направление может быть задано в градусах относительно какой-то фиксированной оси или вектора.
Например, если точка движется по прямой линии от начальной точки к конечной точке, то направление может быть задано как "вперед" или "назад". Если точка движется по окружности, то направление указывает на то, в каком направлении она обходит окружность (по часовой или против часовой стрелки).
Модуль вектора скорости указывает на скорость движения точки. Модуль может быть задан в метрах в секунду, километрах в час или других единицах измерения скорости. Чем больше модуль вектора скорости, тем быстрее движется точка.
Направление движения точки может меняться со временем. Например, точка может двигаться по прямой линии, а затем совершить поворот и двигаться по другой прямой линии. В этом случае, вектор скорости будет меняться в соответствии с новым направлением движения.
Направление движения точки может быть также связано с другими физическими величинами. Например, если точка движется под действием силы тяжести, то направление движения будет задано вниз, в сторону географического центра Земли.
Определение вектора движения
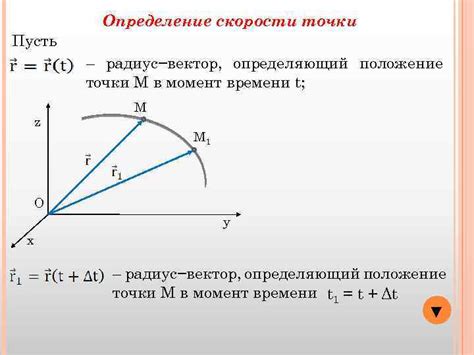
Вектор движения используется для описания перемещения объекта в пространстве. Он представляет собой направление и длину перемещения.
Для определения вектора движения необходимо знать начальное и конечное положение объекта, а также время, за которое объект переместился.
Для нахождения вектора движения можно использовать следующую формулу:
Вектор движения = (Конечное положение - Начальное положение) / Время
Данная формула позволяет определить не только направление, но и скорость перемещения объекта.
Также вектор движения можно представить в виде координат, где каждая координата описывает перемещение объекта по соответствующей оси.
Например, если объект перемещается на 5 метров вправо и на 3 метра вверх за время 2 секунды, то можно записать вектор движения в виде (5, 3).
Вектор движения имеет такие характеристики как длина, направление и ориентация.
Длина вектора движения определяется как квадратный корень из суммы квадратов его координат.
Направление вектора движения определяется углом между его направлением и положительным направлением оси.
Ориентация вектора движения указывает на его направление от начального положения к конечному положению.
Влияние сил на путь точки
Силы, действующие на точку, могут значительно влиять на ее путь и положение. В физике выделяют несколько основных типов сил:
- Гравитационная сила - сила притяжения Земли;
- Тяготение - сила притяжения других объектов;
- Силы трения - силы, препятствующие движению точки на поверхности;
- Силы упругости - силы, возникающие при деформации объектов;
- Электромагнитные силы - силы, связанные с электрическими и магнитными полями.
Каждая из этих сил может оказывать определенное влияние на траекторию точки:
- Гравитационная сила будет притягивать точку к Земле и определять направление движения вниз;
- Тяготение со стороны других объектов может изменить направление движения точки;
- Силы трения могут замедлить скорость движения точки и изменить его направление;
- Силы упругости могут вызывать отскок точки при достижении определенного предела;
- Электромагнитные силы могут оказывать воздействие на точку в зависимости от ее заряда и положения относительно электрических или магнитных полей.
Сочетание влияний разных сил может создавать сложные траектории точки. Например, если на точку действуют гравитационная сила и сила трения, она будет двигаться по криволинейной траектории с учетом направления сил. Если к этим силам добавляется сила упругости, то траектория может стать еще более сложной.
Таким образом, путь и положение точки могут быть определены не только начальной скоростью и направлением движения, но и силами, действующими на нее. Понимание влияния сил на траекторию точки позволяет более точно предсказывать ее движение и использовать эту информацию в различных научных и технических задачах.
Скорость перемещения точки
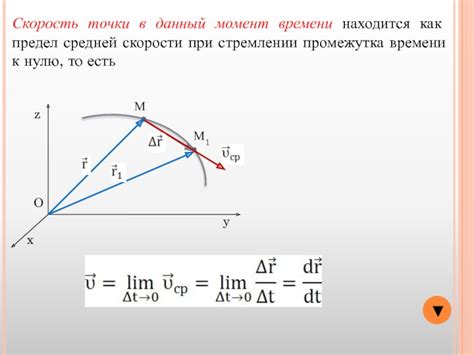
Скорость перемещения точки является векторной величиной, которая характеризует изменение положения точки в зависимости от времени. Она определяется как отношение пройденного пути к затраченному времени:
Скорость = Пройденный путь / Время
Единица измерения скорости в Международной системе единиц (СИ) обычно выбирается метр в секунду (м/с), однако для удобства в некоторых случаях используются другие единицы, например, километр в час (км/ч) или метр в минуту (м/мин).
Скорость перемещения точки может быть постоянной (равномерной) или переменной (неравномерной). В случае равномерного движения скорость точки остается постоянной в течение всего времени перемещения. В случае неравномерного движения скорость точки изменяется со временем.
Чтобы определить скорость перемещения точки, необходимо знать пройденный путь и время, затраченное на это. Пройденный путь можно найти, зная начальное и конечное положение точки. Время можно измерить с помощью хронометра или других средств измерения времени.
Определение скорости перемещения точки важно для анализа различных физических явлений, таких как движение тел, транспортные процессы, а также для решения различных задач из различных областей науки и техники.
Средняя скорость и путь движения
Для вычисления средней скорости движения точки за 6 секунд, необходимо знать начальное положение точки и положение, которое она занимает через указанный промежуток времени.
Средняя скорость вычисляется по следующей формуле:
Скорость = (Изменение пути) / (Изменение времени)
Изменение пути можно определить вычислением разности координат точки на начальный и конечный моменты времени. Например, если начальное положение точки - (2, 3), а положение после 6 секунд - (8, 10), то разница в координатах будет (8-2, 10-3) = (6, 7).
Изменение времени в данном случае равно 6 секундам.
Подставив значения в формулу, получим:
Скорость = (6, 7) / 6 = (1,17, 1,17)
Таким образом, средняя скорость точки за указанный промежуток времени составляет примерно 1,17 единицы расстояния в секунду.
Путь движения точки за 6 секунд можно определить как расстояние между начальным и конечным положением точки.
В данном случае, путь равен длине вектора изменения пути, то есть квадратному корню из суммы квадратов разности координат точки:
Путь = √((6^2)+(7^2)) ≈ 9.22 единицы расстояния
Таким образом, точка переместилась на примерно 9.22 единицы в указанном направлении за 6 секунд.
Мгновенная скорость и изменение пути

Мгновенная скорость - это скорость в конкретный момент времени. Во время движения точки ее скорость может меняться. Изменение пути - это разность между путями, которые точка прошла за два разных промежутка времени. Рассмотрим эти понятия более подробно.
Мгновенная скорость можно определить, разделив перемещение на очень малый промежуток времени. Если точка переместилась на расстояние Δx за время Δt, то мгновенная скорость v в этот момент времени определяется как v = Δx/Δt.
Изменение пути можно вычислить следующим образом: Δs = sконечное - sначальное, где sконечное - конечный путь, пройденный точкой, sначальное - начальный путь, пройденный точкой.
Если изменение пути положительное, то это означает, что точка переместилась вперед относительно своего начального положения. Если изменение пути отрицательное, то это означает, что точка переместилась назад относительно своего начального положения.
Таблица ниже показывает примеры изменений пути для точки, которая движется вперед и назад:
| Мгновенная скорость | Изменение пути |
|---|---|
| Положительная | Положительное |
| Положительная | Отрицательное |
| Отрицательная | Положительное |
| Отрицательная | Отрицательное |
Важно понимать, что мгновенная скорость и изменение пути могут быть положительными, отрицательными или равными нулю в зависимости от направления движения точки и изменения положения.
Расчет конечной координаты точки
Для расчета конечной координаты точки, необходимо знать начальные координаты точки и ее скорость. Зная эти два параметра, можно применить формулу перемещения точки для определения конечной координаты.
Формула перемещения точки имеет вид:
к = к0 + v * t
- к - конечная координата точки
- к0 - начальная координата точки
- v - скорость точки
- t - время движения точки
Где:
- Начальная координата точки (к0) - это ее положение в начале движения.
- Скорость точки (v) - это величина, определяющая изменение координаты точки за единицу времени.
- Время движения точки (t) - это промежуток времени, в течение которого происходит перемещение точки.
Таким образом, для расчета конечной координаты точки необходимо умножить скорость на время движения и прибавить эту величину к начальной координате точки.
Учет времени и скорости
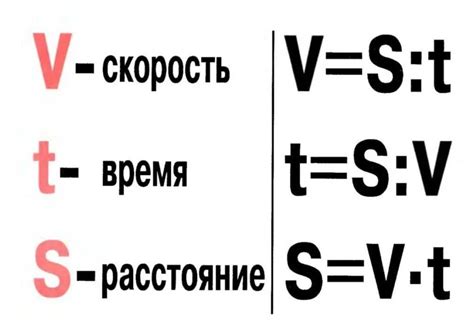
При перемещении точки за определенное время необходимо учитывать и скорость движения. Скорость определяет, как много пути будет преодолено за единицу времени. Для учета времени и скорости можно использовать простую формулу.
Если скорость постоянна, то пройденный путь равен произведению скорости на время: путь = скорость * время.
Если скорость не постоянна, то пройденный путь можно разбить на более маленькие участки, для которых скорость будет постоянной. Затем для каждого участка следует вычислить пройденный путь с помощью формулы путь = скорость * время. Итоговый пройденный путь будет равен сумме пройденных участков.
Для более точного учета времени и скорости можно использовать интервальное измерение, когда время разбивается на равные интервалы. На каждом интервале скорость и пройденный путь могут быть разными, поэтому для каждого интервала следует вычислять пройденный путь с помощью формулы путь = скорость * время. Итоговый пройденный путь будет равен сумме пройденных участков.
Для более наглядного представления данных об учете времени и скорости можно использовать таблицу. В таблице можно указать время, скорость и пройденный путь для каждого интервала или участка. Также можно использовать диаграммы или графики для визуализации данных о перемещении точки.
Вопрос-ответ
Какая формула позволяет вычислить перемещение точки за 6 секунд?
Формула для вычисления перемещения точки за определенный период времени представляет собой произведение скорости на время. Если известна начальная и конечная точки движения, можно использовать формулу расстояния между двумя точками в пространстве.
Как определить положение точки после 6 секунд движения?
Для определения положения точки после 6 секунд движения необходимы данные о начальном положении точки и ее скорости. С использованием формулы расчета пути можно вычислить изменение положения точки за заданное время.
Как определить путь, пройденный точкой за 6 секунд?
Для определения пути, пройденного точкой за 6 секунд, необходимо знать ее скорость. Путь можно рассчитать, умножив модуль скорости на время.