При работе с вероятностными моделями важно понимать, что задание правильного закона распределения является ключевым шагом в анализе случайных явлений. Существует несколько способов, которые НЕ рекомендуется использовать при задании закона распределения.
Во-первых, не следует основываться исключительно на интуиции или предположениях. Хотя в некоторых случаях интуиция может быть полезной, она не может заменить строгого анализа данных и математических методов. Использование интуитивных предположений может привести к неправильным выводам и искаженной картине закона распределения.
Во-вторых, не рекомендуется использовать случайные выборки для определения закона распределения. Случайные выборки могут быть полезны для получения информации о конкретной выборке данных, но они не могут использоваться для обобщения на все возможные значения. Случайная выборка может не содержать всех возможных значений, и, следовательно, может давать неполную картину закона распределения.
В-третьих, не рекомендуется использовать априорные предположения без подтверждения. Априорные предположения могут быть полезны для начального задания закона распределения, но они должны быть проверены и подтверждены эмпирическими данными. Использование неподтвержденных априорных предположений может привести к искаженным результатам и неправильному анализу данных.
В заключение, для задания закона распределения следует использовать строгое математическое моделирование и анализ данных, а также проверять и подтверждать априорные предположения. Интуиция и случайные выборки должны быть использованы с осторожностью и в сопоставлении с надежными математическими методами.
Проблема задания закона распределения
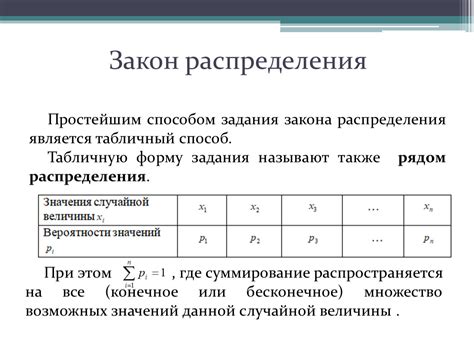
При изучении вероятностных явлений и статистики важной задачей является задание закона распределения случайной величины. Закон распределения описывает вероятности возможных значений случайной величины и позволяет проводить различные статистические анализы.
Однако, существуют способы задания закона распределения, которые не применяются из-за своей непригодности для описания вероятностных явлений. Эти способы включают:
- Несогласованные законы распределения: в этом случае задается закон распределения, который не соответствует характеру случайной величины или нарушает условия применимости.
- Отрицательные вероятности: законы распределения, в которых присутствуют отрицательные вероятности, также не применяются. Вероятность не может быть меньше нуля, поэтому такие законы не имеют смысла и не могут быть использованы для анализа данных.
- Недостаточная информация: если о законе распределения известна недостаточная информация, то он не может быть задан полностью и, следовательно, не может быть использован.
- Произвольное задание: случайный выбор или произвольное задание закона распределения без всякого обоснования также не применяются. Вероятностные явления должны быть основаны на данных и доказательствах.
Таким образом, при задании закона распределения необходимо учитывать его согласованность с характером случайной величины, отсутствие отрицательных вероятностей и наличие достаточной информации. Также важно основывать закон распределения на данных и доказательствах, а не произвольно выбирать его.
Шумы и отклонения от нормала
При описании закона распределения случайной величины важно учитывать возможные шумы и отклонения от ожидаемого идеального закона.
Шумы и отклонения могут возникать по разным причинам, например, из-за ошибок измерений, неполной информации или случайных факторов, которые не учтены при построении закона распределения.
Для более точного описания случайной величины и ее закона распределения могут использоваться различные методы анализа данных, такие как статистические исправления, фильтрация шумов, аппроксимация функциями или применение других математических моделей.
Однако следует отметить, что при использовании таких методов может возникнуть определенная степень неточности или приближения в описании закона распределения. Поэтому для получения более точных результатов необходимо учитывать возможные шумы и отклонения в данных и применять соответствующие методы и модели для их учета.
Теория игнорируемости парных характеристик
Теория игнорируемости парных характеристик является одним из способов анализа и моделирования данных. Она основана на предположении о независимости исследуемых характеристик в наборе данных. Суть теории заключается в том, что при задании закона распределения одной из парных характеристик можно игнорировать влияние остальных парных характеристик.
Применение теории игнорируемости парных характеристик позволяет упростить статистический анализ данных, так как можно сосредоточиться только на изучении влияния одной переменной на другую, игнорируя все остальные переменные. Это особенно полезно в случае, когда в наборе данных присутствуют множественные зависимости между переменными.
Однако, следует отметить, что теория игнорируемости парных характеристик имеет свои ограничения. Во-первых, она предполагает, что каждая переменная описывается нормальным распределением. Во-вторых, она не учитывает возможные зависимости между тройками или группами переменных.
В связи с этим, перед применением теории игнорируемости парных характеристик необходимо тщательно проверить данные на соответствие предположениям этой теории и учитывать возможные ограничения при интерпретации результатов анализа.
Непрерывность и вероятность равенства
При задании закона распределения случайной величины могут использоваться различные способы, однако некоторые из них не применяются в контексте непрерывных случайных величин и вероятности равенства.
- Способ задания через таблицу значений: при помощи данного способа можно описать лишь дискретную случайную величину, для которой существует конечное или счетное число возможных значений. Однако для непрерывных случайных величин число возможных значений является несчетным бесконечным множеством.
- Способ задания через функцию распределения: данный способ применим для любой случайной величины, но он не позволяет задать конкретную вероятность выпадения какого-либо конкретного значения, а только вероятность попадания случайной величины в заданный интервал.
Таким образом, при задании закона распределения непрерывных случайных величин не применяются способы через таблицу значений и через функцию распределения, которые могут быть применены только для дискретных случайных величин.
Внешние факторы
При задании закона распределения определенной случайной величины не применяются следующие способы, связанные с внешними факторами:
- Переоценка ситуации: Не рекомендуется изменять или искажать исходные данные и параметры распределения случайной величины на основе личных предпочтений, субъективных оценок или необоснованных домыслов.
- Произвольное выборочное исследование: Не рекомендуется выбирать лишь определенное подмножество из общей генеральной совокупности или произвольно изменять размер выборки при изучении закона распределения. Это может привести к искажению исследуемых данных и неправильному представлению о характеристиках случайной величины.
- Несоответствие статистическим методам: Не рекомендуется использовать статистические методы неправильно или применять их без учета особенностей задачи и конкретных условий. Это может привести к неверным результатам и неверной интерпретации полученных данных.
- Игнорирование внешних факторов: Не рекомендуется пренебрегать внешними факторами, которые могут оказывать влияние на исследуемую случайную величину. Необходимо учитывать все возможные факторы, которые могут влиять на закон распределения, чтобы избежать ошибочных выводов.
Все эти внешние факторы могут искажать результаты и приводить к неверным выводам при задании закона распределения случайной величины. Поэтому необходимо быть внимательным при выборе методов и подходов к заданию закона распределения и учитывать все внешние факторы, которые могут влиять на исследуемую случайную величину.
Игнорирование зависимостей
При задании закона распределения случайной величины нельзя игнорировать зависимости между различными факторами, которые могут влиять на результаты. Игнорирование зависимостей может привести к неправильному определению вероятностей и искажению закона распределения.
Например, при изучении влияния факторов на прибыль компании нельзя пренебрегать взаимосвязью между объемом продаж и рекламными затратами. Если величины этих двух факторов зависят друг от друга, то игнорирование этой зависимости может привести к недостоверным результатам.
Чтобы избежать игнорирования зависимостей при задании закона распределения, необходимо анализировать все существующие взаимосвязи между факторами и учитывать их в моделировании. Это может потребовать дополнительных данных и более сложных методов статистического анализа.
Вопрос-ответ
Какой способ использовать для задания закона распределения?
Для задания закона распределения можно использовать несколько способов, включая методы математической статистики, эмпирическую оценку и моделирование.
Какие способы не рекомендуется использовать для задания закона распределения?
Не рекомендуется использовать методы случайного выбора или субъективные предположения для задания закона распределения. Это может привести к неточным результатам и ошибкам в анализе данных.
Можно ли задать закон распределения простым перечислением значений?
Да, можно задать закон распределения простым перечислением значений. Этот способ называется дискретным распределением, и он применяется, когда возможные значения случайной величины известны и ограничены.
Какое преимущество имеет использование математической статистики для задания закона распределения?
Использование математической статистики позволяет определить закон распределения на основе статистических данных, таких как выборочные средние и дисперсии. Это дает более объективные и надежные результаты, чем субъективные предположения или случайный выбор значений.