Синус и косинус - математические функции, которые играют важную роль в физике. Они появляются во многих физических законах и уравнениях, таких как уравнение движения, законы вещественной оптики и электромагнитной теории.
Синус и косинус - это функции угла, которые вычисляют соотношение сторон треугольника. Для любого треугольника, угол и противоположная сторона связаны между собой. С помощью синуса и косинуса мы можем определить соотношение между углом и противоположной стороной.
В этой статье мы рассмотрим, как использовать синус и косинус в физике. Мы охватим основные концепции и применения этих функций в физических задачах. Кроме того, мы рассмотрим, как использовать таблицы синусов и косинусов, чтобы упростить вычисления.
Основы геометрии
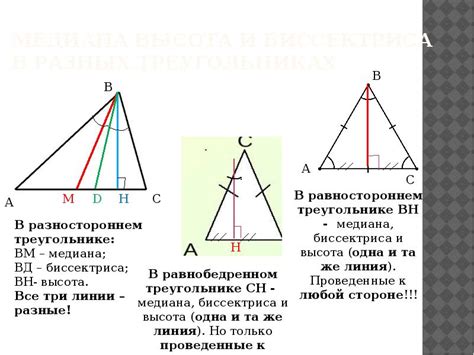
Геометрия – наука о форме, размерах и расположении фигур в пространстве. Она основывается на задании фигур в координатном пространстве с помощью алгебраических уравнений.
Тригонометрия – раздел геометрии, который изучает соотношения между сторонами и углами треугольников. Он используется в различных науках, включая физику, технику и математику.
Тригонометрические функции, такие как sin, cos и tan, используются для вычисления сторон и углов треугольников и других геометрических фигур.
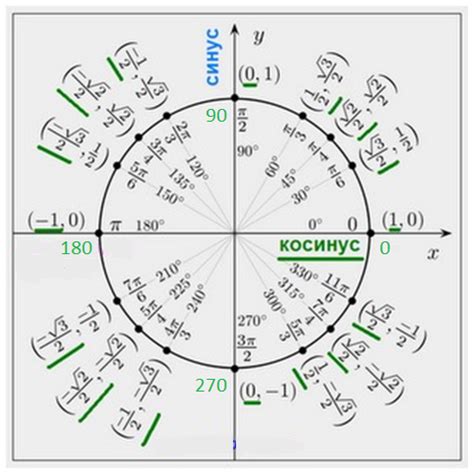
Тригонометрический круг – это геометрическая фигура, которая показывает значения тригонометрических функций в зависимости от угла. Синус и косинус зависят от определенных значений угла, которые можно выразить в радианах.
Формула Пифагора – это основное утверждение геометрии, которое гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Она широко используется в физике для определения расстояний и скоростей.
Геометрические преобразования – это действия над фигурами, которые сохраняют их геометрические свойства. Они включают повороты, симметрии и преобразования в виде гомотетии.
Синус и косинус: определения и свойства
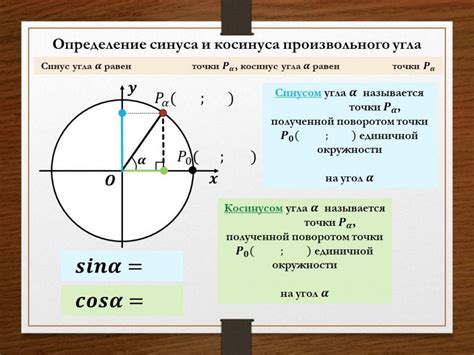
Синус и косинус - это тригонометрические функции, определенные на основе прямоугольного треугольника. Для любого угла α (в радианах) на плоскости, синус α равен отношению длины противолежащего катета к гипотенузе, а косинус α равен отношению длины прилежащего катета к гипотенузе.
Формально, синус α записывается как sin α, а косинус α записывается как cos α. Обе функции могут принимать любое значение от -1 до 1, и каждая функция является периодической с периодом 2π радиан.
Синус и косинус используются в различных областях физики, таких как механика, оптика, электротехника и другие. Они используются для описания колебаний, волн, движения и электрических сигналов.
Свойства синуса и косинуса включают аддитивность, четность, нечестность, периодичность и многие другие. Они обладают также формулами двойного угла, половинного угла и другими тригонометрическими идентичностями.
Знание синуса и косинуса является ключевым для различных задач, которые могут возникнуть в повседневной жизни и при изучении физики. Они также могут использоваться для решения сложных математических задач, таких как дифференциальные уравнения и другие.
Как использовать sin и cos в физике: расчёт векторных проекций
Векторные проекции имеют большое значение в физике и могут применяться для вычисления таких параметров, как сила, скорость, ускорение и импульс. Использование sin и cos в расчёте векторных проекций позволяет получить точные данные о направлениях и величинах векторов.
Для расчёта векторных проекций необходимо знать угол, под которым вектор проецируется на другой вектор. Этот угол можно найти с помощью функций sin и cos. Например, для расчёта проекции вектора A на вектор B необходимо найти угол между векторами и вычислить cos этого угла. Затем, перемножив величину вектора A на cos угла, получится значение проекции.
Для расчёта проекции, перпендикулярной вектору B, нужно использовать sin угла между векторами. В этом случае величина проекции будет равна произведению величины вектора A на sin угла между векторами.
Важно знать, что значения sin и cos зависят от единицы измерения угла. В научных расчётах обычно используется радианная мера угла. Поэтому перед подсчётом проекций необходимо перевести градусы в радианы с помощью формулы: радианы = градусы * π / 180.
Наконец, при использовании sin и cos необходимо помнить об их обратных функциях, arcsin и arccos, которые позволяют найти угол по заданным значениям проекций.
Как использовать sin и cos в физике: расчёт сил и напряжений
Синус и косинус - это тригонометрические функции, которые нашли свое применение во многих математических и физических задачах. В физике, особенно в механике и электротехнике, они используются для расчета сил и напряжений в системах.
Силы, действующие на тело, могут быть разложены на две составляющие: горизонтальную и вертикальную. Для расчета этих составляющих используются соответствующие тригонометрические функции. Так, сила F, направленная под углом a к горизонту, может быть разложена на Fx и Fy.
Косинус угла a используется для расчета Fx: Fx = F cos(a). А синус угла a - для расчета Fy: Fy = F sin(a). Таким образом, можно вычислить компоненты силы F в любой системе координат.
Напряжения в электрических цепях также можно выразить через синус и косинус. Напряжение - это разность потенциалов между двумя точками в цепи. Если известны напряжение и угол между точками, можно вычислить активную и реактивную составляющую напряжения.
Активная составляющая напряжения выражается через косинус угла: Ua = U cos(a). А реактивная составляющая - через синус угла: Ur = U sin(a).
Также, с помощью тригонометрических функций можно вычислить фазовый угол в цепи, который является важным параметром в электротехнике. Фазовый угол определяет сдвиг фаз между напряжением и током в цепи и влияет на многие характеристики электрических устройств.
- Выводы:
Тригонометрические функции sin и cos находят широкое применение в физических задачах.
Используя синус и косинус, можно разложить силу на составляющие и вычислить компоненты в любой системе координат.
В электротехнике с помощью синуса и косинуса можно выразить напряжения и вычислить фазовый угол в цепи.
Применение sin и cos в механике: определение перемещения
Применение sin и cos в механике существенно упрощает определение перемещения тела в пространстве. Рассмотрим пример: тело движется по прямой линии, его начальная скорость равна V0, а угол, образованный направлением движения тела и осью X, равен α.
С использованием тригонометрии мы можем определить проекцию скорости на ось X, используя функцию cos. Проекция скорости на ось Y определяется с помощью функции sin.
Далее, зная проекции скорости на оси X и Y, мы можем рассчитать перемещение тела за промежуток времени t. Проекция перемещения на ось X определяется умножением проекции скорости на ось X на промежуток времени t, проекция на ось Y - умножением проекции скорости на ось Y на промежуток времени t.
Таким образом, применение sin и cos в механике позволяет определять перемещение тела в пространстве, используя знания о направлении движения тела и его начальной скорости. Это очень важный инструмент в работе физика или инженера.
Применение sin и cos в электронике: расчёт периодических сигналов
Функции синуса и косинуса имеют широкое применение в электронике. Они используются, например, для расчета периодических сигналов, таких как аналоговые сигналы в звуковых системах, видеосигналы на телевизорах и многие другие.
Для расчета периодических сигналов используется формула, которая выражается через функции синуса и косинуса. Ее можно использовать, чтобы определить, насколько быстро будет меняться сигнал и как он будет выглядеть на графике.
Например, если вы хотите создать сигнал с частотой 100 Гц, то вы можете использовать формулу, которая выражается через функцию синуса и косинуса. В этом случае, для создания такого сигнала вам нужно определить амплитуду, фазу и частоту сигнала.
Таким образом, знание функций синуса и косинуса является необходимым в электронике для создания и анализа периодических сигналов, обработки сигналов и других приложений.
Применение sin и cos в оптике: расчёт положения искажений в линзах

Оптика - это раздел физики, изучающий распространение света и его взаимодействие с веществом. Один из основных элементов оптической системы - это линзы. Они используются для фокусировки, изменения масштаба и искажения изображений.
Расчет положения искажений в линзах возможен благодаря использованию sin и cos. Для этого необходимо знать формулу тонкой линзы:
1/f = (n - 1) * (1/R1 - 1/R2)
- f - фокусное расстояние линзы
- n - показатель преломления вещества линзы
- R1 и R2 - радиусы кривизны поверхностей линзы
Для расчета положения искажений, необходимо использовать следующие формулы:
u = y'/y = (M + 1) / M
v = x'/x = M / (M + 1)
- u - увеличение по вертикали
- v - увеличение по горизонтали
- y' - размер изображения
- y - размер предмета
- x' - размер изображения
- x - размер предмета
- M - линейное увеличение
С помощью этих формул можно рассчитать параметры изображений, создаваемых линзами. Это важно для многих областей, таких как астрономия, микроскопия, фотография и другие, где точность искажений является критически важным фактором.
Общие сведения о тригонометрии: другие функции и применение в физике
Вместе с sin и cos, тригонометрические функции включают еще несколько функций, таких как tan (тангенс), cot (котангенс), sec (секанс) и csc (косеканс).
Тангенс и котангенс вычисляются как отношение синуса и косинуса соответственно. Они зачастую используются в геометрии и физике для вычисления углов, ускорения и скорости векторов.
Секанс и косеканс являются взаимными функциями косинуса и синуса соответственно. Они встречаются реже, но находят применение в некоторых задачах физики.
Тригонометрические функции используются в физике для расчета колебаний, волн, электромагнитных полей и других физических явлений. Например, они используются для описания колебаний звуковых волн и электромагнитных волн в вакууме.
Также, тригонометрические функции используются в различных областях инженерии и техники, таких как строительство мостов и дизайн автомобилей.
В целом, знание тригонометрии является важной составляющей для понимания физических явлений и их математической моделирования.
Вопрос-ответ
Что такое sin и cos в физике?
Sin и cos - это тригонометрические функции, которые используются для описания связи между углом и длиной сторон треугольника. В физике они используются для решения задач в различных областях, таких как механика, электричество и магнетизм, оптика и другие.
Как использовать sin и cos в механике?
В механике sin и cos используются для описания движения тела по окружности. Они могут помочь определить расстояние, пройденное телом, угол поворота и скорость. Например, если известны угол поворота и радиус окружности, можно определить, какой путь пройдет тело.
Как использовать sin и cos в оптике?
В оптике sin и cos используются для определения показателя преломления и угла преломления света при переходе из одной среды в другую. Они также помогают определить фазовый сдвиг, который возникает при отражении и преломлении света.
Как находить сумму и разность sin и cos?
Сумма sin и cos может быть найдена с помощью формулы sin(a+b) = sin(a)cos(b) + cos(a)sin(b), а разность с помощью формулы sin(a-b) = sin(a)cos(b) - cos(a)sin(b). Также можно использовать тригонометрический круг, который помогает найти значения sin и cos для всех углов.
Как использовать sin и cos в электричестве и магнетизме?
В электричестве и магнетизме sin и cos используются для описания электрических и магнитных сигналов. Они также используются для определения напряжения и тока в цепи, а также для нахождения мощности и энергии. Формулы, которые используют sin и cos, также позволяют определить индуктивность и емкость электрических цепей.